题目内容
如图，在△ABC，AC⊥BC，D是BC延长线上的一点，E是AC上的一点，连接ED，∠A=∠D．
求证：△ABC∽△DEC．
证明：∵AC⊥BC，
∴∠ACB=∠DCE=90°，
又∵∠A=∠D，
∴△ABC∽△DEC．
分析：利用两角法即可判断出△ABC∽△DEC．
点评：本题考查了相似三角形的判定，属于基础题，注意相似三角形的判定可以是：两角法，两边及其夹角法，三边法．
∴∠ACB=∠DCE=90°，
又∵∠A=∠D，
∴△ABC∽△DEC．
分析：利用两角法即可判断出△ABC∽△DEC．
点评：本题考查了相似三角形的判定，属于基础题，注意相似三角形的判定可以是：两角法，两边及其夹角法，三边法．
练习册系列答案
名校课堂系列答案
相关题目
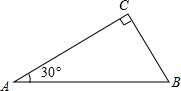的顶点D放在AB边上，E、F分别在AC、BC上，当点D在AB边上移动时，DE始终与AB垂直．
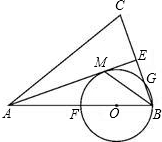F，FB恰为⊙O的直径．
7、如图，在△ABC中，D是BC上的一点，∠C=62°，∠CAD=32°，则∠ADB=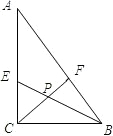
如图，在△ABC中，∠ACB=90°，BE平分∠ABC，CF平分∠ACB，CF，BE交于点P，AC=4cm，BC=3cm，AB=5cm，则△CPB的面积为
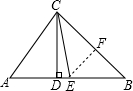如图，在△ABC中，CD是高，CE为∠ACB的平分线．若AC=15，BC=20，CD=12，EF∥AC，则∠CEF的大小为