题目内容
如图，△ABC的面积为60，点0是重心，连接BG并延长交AC于D，连接GA，则△GAB的面积为
- A.40
- B.30
- C.20
- D.10
C
分析：连接CG并延长交AB于点E，根据G是△ABC的重心可知EG=
CE，再根据三角形的面积公式即可求解．
解答：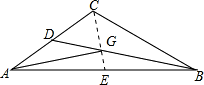
解：连接CG并延长交AB于点E，
∵G是△ABC的重心，
∴GE=CE
∴S△GAB=S△ABC=×60=20．
故选C．
点评：本题考查的是三角形的重心及三角形的面积公式，熟知三角形重心的特点是解答此题的关键．
分析：连接CG并延长交AB于点E，根据G是△ABC的重心可知EG=
CE，再根据三角形的面积公式即可求解．解答：
解：连接CG并延长交AB于点E，∵G是△ABC的重心，
∴GE=
CE∴S△GAB=
S△ABC=×60=20．故选C．
点评：本题考查的是三角形的重心及三角形的面积公式，熟知三角形重心的特点是解答此题的关键．
练习册系列答案
相关题目
如图，△ABC的面积是63，D是BC上的一点，且BD：CD=2：1，DE∥AC交AB于E，延长DE到F，使FE：ED=2：1，则△CDF的面积是
如图，△ABC的面积为1，分别取AC、BC两边的中点A1、B1，则四边形A1ABB1的面积为
如图，△ABC的面积为
3、如图，△ABC的面积为1，若把△ABC的各边分别延长一倍，得到一个新的△DEF，则S△DEF=
如图，△ABC的面积为1．第一次操作：分别延长AB，BC，CA至点A1，B1，C1，使A1B=AB，B1C=BC，C1A=CA，顺次连结A1，B1，C1，得到△A1B1C1．第二次操作：分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连结A2，B2，C2，得到△A2B2C2．…按此规律，要使得到的三角形的面积超过2013，最少经过