题目内容
(2012•昌平区二模)如图所示,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别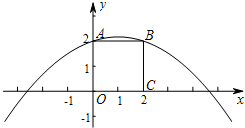 在y轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,
在y轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,
).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找到点M,使得M到D、B的距离之和最小,求出点M的坐标;
(3)如果点P由点A出发沿线段AB以2cm/s的速度向点B运动,同时点Q由点B出发沿线段BC以1cm/s的速度向点C运动,当其中一点到达终点时,另一点也随之停止运动.设S=PQ2(cm2).
①求出S与运动时间t之间的函数关系式,并写出t的取值范围;
②当S=
时,在抛物线上存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形,求出点R的坐标.
 在y轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,
在y轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,| 2 |
| 3 |
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找到点M,使得M到D、B的距离之和最小,求出点M的坐标;
(3)如果点P由点A出发沿线段AB以2cm/s的速度向点B运动,同时点Q由点B出发沿线段BC以1cm/s的速度向点C运动,当其中一点到达终点时,另一点也随之停止运动.设S=PQ2(cm2).
①求出S与运动时间t之间的函数关系式,并写出t的取值范围;
②当S=
| 5 |
| 4 |
分析:(1)设抛物线的解析式是y=ax2+bx+c,求出A、B、D的坐标代入即可;
(2)A关于抛物线的对称轴的对称点为B,过B、D的直线与抛物线的对称轴的交点为所求M,求出直线BD的解析式,把抛物线的对称轴x=1代入即可求出M的坐标;
(3)①根据勾股定理和已知条件,可以求得PB、BQ的长度,即可求出S与运动时间t之间的函数关系式(0≤t≤1);
②假设存在点R,可构成以P、B、R、Q为顶点的平行四边形,求出P、Q的坐标,再分为两种种情况根据平行四边形的性质求出R点的坐标,代入抛物线解析式,看能否使等式成立,能的话,这种情况就存在.
(2)A关于抛物线的对称轴的对称点为B,过B、D的直线与抛物线的对称轴的交点为所求M,求出直线BD的解析式,把抛物线的对称轴x=1代入即可求出M的坐标;
(3)①根据勾股定理和已知条件,可以求得PB、BQ的长度,即可求出S与运动时间t之间的函数关系式(0≤t≤1);
②假设存在点R,可构成以P、B、R、Q为顶点的平行四边形,求出P、Q的坐标,再分为两种种情况根据平行四边形的性质求出R点的坐标,代入抛物线解析式,看能否使等式成立,能的话,这种情况就存在.
解答:解:(1)据题意可知:A(0,2),B(2,2),C(2,0).
∵抛物线y=ax2+bx+c经过点A、B和D(4,
),
∴
,
∴
,
∴y=-
x2+
x+2;
(2)点B关于抛物线的对称轴x=1的对称点为A.
连接AD,与对称轴的交点即为M.
∵A(0,2)、D(4,
),
∴直线AD的解析式为:y=-
x+2,
当x=1时,y=
,
则M(1,
);
(3)①由图象知:PB=2-2t,BQ=t,AP=2t,
∵在Rt△PBQ中,∠B=90°,
∴S=PQ2=PB2+BQ2,
∴=(2-2t)2+t2,
即S=5t2-8t+4(0≤t≤1).
②当S=
时,
=5t2-8t+4
即20t2-32t+11=0,
解得:t=
,t=
>1(舍)
∴P(1,2),Q(2,
).
∴PB=1.
若R点存在,分情况讨论:
(i)假设R在BQ的右边,如图所示,这时QR=PB,RQ∥PB,
则R的横坐标为3,R的纵坐标为
,
即R(3,
),代入y=-
x2+
x+2,左右两边相等,
故这时存在R(3,
)满足题意;
(ii)假设R在PB的左边时,这时PR=QB,PR∥QB,
则R(1,
)代入y=-
x2+
x+2,左右两边不相等,
则R不在抛物线上
综上所述,存点一点R,以点P、B、Q、R为顶点的平行四边形只能是□PQRB.
则R(3,
).
此时,点R(3,
)在抛物线=-
x2+
x+2上.
∵抛物线y=ax2+bx+c经过点A、B和D(4,
| 2 |
| 3 |
∴
|
∴
|
∴y=-
| 1 |
| 6 |
| 1 |
| 3 |
(2)点B关于抛物线的对称轴x=1的对称点为A.
连接AD,与对称轴的交点即为M.
∵A(0,2)、D(4,
| 2 |
| 3 |

∴直线AD的解析式为:y=-
| 1 |
| 3 |
当x=1时,y=
| 5 |
| 3 |
则M(1,
| 5 |
| 3 |
(3)①由图象知:PB=2-2t,BQ=t,AP=2t,
∵在Rt△PBQ中,∠B=90°,
∴S=PQ2=PB2+BQ2,
∴=(2-2t)2+t2,
即S=5t2-8t+4(0≤t≤1).
②当S=
| 5 |
| 4 |
| 5 |
| 4 |
即20t2-32t+11=0,
解得:t=
| 1 |
| 2 |
| 11 |
| 10 |
∴P(1,2),Q(2,
| 3 |
| 2 |
∴PB=1.
若R点存在,分情况讨论:
(i)假设R在BQ的右边,如图所示,这时QR=PB,RQ∥PB,
则R的横坐标为3,R的纵坐标为
| 3 |
| 2 |
即R(3,
| 3 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
故这时存在R(3,
| 3 |
| 2 |
(ii)假设R在PB的左边时,这时PR=QB,PR∥QB,
则R(1,
| 5 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
则R不在抛物线上
综上所述,存点一点R,以点P、B、Q、R为顶点的平行四边形只能是□PQRB.
则R(3,
| 3 |
| 2 |
此时,点R(3,
| 3 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
点评:本题主要考查了用待定系数法求一次函数和二次函数的解析式,勾股定理,平行四边形的性质,二次函数图象上点的坐标特征等知识点,解此题的关键是综合运用这些知识进行计算.此题综合性强,是一道难度较大的题目.

练习册系列答案
相关题目
 (2012•昌平区二模)如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠ABC=70°,则∠BDC的度数为( )
(2012•昌平区二模)如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠ABC=70°,则∠BDC的度数为( )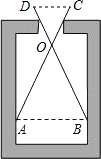 (2012•昌平区二模)如图,用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC:OA=1:2,量得CD=10,则零件的内孔直径AB长为( )
(2012•昌平区二模)如图,用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC:OA=1:2,量得CD=10,则零件的内孔直径AB长为( ) (2012•昌平区二模)如图的方格纸中,每个小方格都是边长为1的正方形,A、B两点是方格纸中的两个格点,在4×5的方格纸中,找出格点C,使△ABC的面积为1个平方单位,则满足条件的格点C的个数是
(2012•昌平区二模)如图的方格纸中,每个小方格都是边长为1的正方形,A、B两点是方格纸中的两个格点,在4×5的方格纸中,找出格点C,使△ABC的面积为1个平方单位,则满足条件的格点C的个数是