ĢāÄæÄŚČŻ
”¾ĢāÄæ”æ¼ŗÖŖŅ»“ĪŗÆŹż![]() £¬
£¬
£Ø1£©ĪŽĀŪ kĪŖŗĪÖµ£¬ŗÆŹżĶ¼Ļń±Ų¹ż¶Øµć£¬ĒóøƵćµÄ×ų±ź£»
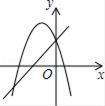
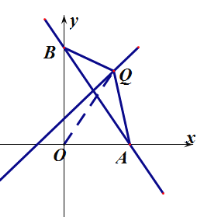
£Ø2£©ČēĶ¼ 1£¬µ± k=-![]() Ź±£¬øĆÖ±Ļß½» x Öį£¬y ÖįÓŚ A£¬B Į½µć£¬Ö±Ļß l2:y=x+1 ½» AB ÓŚµć P£¬µć Q ŹĒ l2 ÉĻŅ»µć£¬Čō SABQ 6 £¬Ēó Q µćµÄ×ų±ź£»
Ź±£¬øĆÖ±Ļß½» x Öį£¬y ÖįÓŚ A£¬B Į½µć£¬Ö±Ļß l2:y=x+1 ½» AB ÓŚµć P£¬µć Q ŹĒ l2 ÉĻŅ»µć£¬Čō SABQ 6 £¬Ēó Q µćµÄ×ų±ź£»
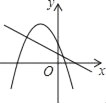
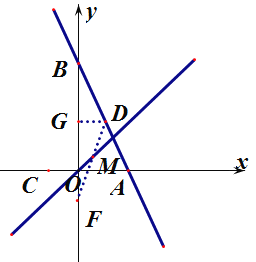
£Ø3£©ČēĶ¼ 2£¬ŌŚµŚ 2 ĪŹµÄĢõ¼žĻĀ£¬ŅŃÖŖ D µćŌŚøĆÖ±ĻßÉĻ£¬ŗį×ų±źĪŖ 1£¬C µćŌŚ x Öįøŗ°ėÖį£¬ ABC=45 £¬¶Æµć M µÄ×ų±źĪŖ£Øa£¬a£©£¬Ēó CM+MD µÄ×īŠ”Öµ£®

”¾“š°ø”æ£Ø1£©(![]() )£»£Ø2£©(3,4)»ņ£Ø-1,0£©£»£Ø3£©
)£»£Ø2£©(3,4)»ņ£Ø-1,0£©£»£Ø3£©![]() £®
£®
”¾½āĪö”æ
£Ø1£©½«Ņ»“ĪŗÆŹż±äŠĪ![]() £¬øł¾ŻĶ¼Ļń¹ż¶Øµć£¬µĆµ½ÓėkÖµĪŽ¹Ų£¬Ēó³ök£¬½ų¶ųĒó³ö¶Øµć×ų±ź£»
£¬øł¾ŻĶ¼Ļń¹ż¶Øµć£¬µĆµ½ÓėkÖµĪŽ¹Ų£¬Ēó³ök£¬½ų¶ųĒó³ö¶Øµć×ų±ź£»
£Ø2£©Ēó³öÖ±Ļß½āĪöŹ½£¬ÉčµćQ×ų±źĪŖ(m,m+1)£»·ÖµćQŌŚABĮ½²ą·ÖĄąĢÖĀŪ¼“æÉ£»
£Ø3£©ĻČøł¾ŻĢāŅā£¬Ēó³öµćC×ų±ź£¬µćD×ų±ź£¬ŌŚøł¾ŻM×ų±źĢŲµć£¬µĆµ½µćMĖłŌŚÖ±Ļß½āĪöŹ½£¬Ēó³öµćC¶Ō³ĘµćF£¬Į¬½ÓDF£¬Ēó³öDF³¤¼“æÉ£®
½ā£ŗ£Ø1£©Ņ»“ĪŗÆŹż![]() £¬
£¬
”ą![]() £¬
£¬
”ß²»ĀŪkĪŖŗĪÖµ£¬ÉĻŹ½¶¼³ÉĮ¢£¬
”ą![]() £¬
£¬![]()
”ą![]() £¬
£¬![]()
”ąĪŽĀŪ k ĪŖŗĪÖµ£¬ŗÆŹż![]() Ķ¼Ļń±Ų¹ż¶Øµć(
Ķ¼Ļń±Ų¹ż¶Øµć(![]() )£»
)£»
£Ø2£©µ± k=-![]() Ź±£¬Ņ»“ĪŗÆŹż
Ź±£¬Ņ»“ĪŗÆŹż![]() ĪŖ
ĪŖ![]() £¬
£¬
µ±x=0Ź±£¬y=4£»µ±y=0£¬Ź±£¬-2x+4=0£¬x=2£»
”ąµćA×ų±źĪŖ(2,0)£»µćB×ų±źĪŖ(0,4)£»
”ßµćQŌŚŌŚÖ±Ļßl2:y=x+1ÉĻ£¬
”ąÉčµćQ×ų±źĪŖ(m,m+1)£»
¢ŁČēĶ¼£¬µ±µćQĪ»ÓŚABÓŅ²ąŹ±£¬øł¾ŻĢāŅāµĆ![]()
”ą![]()
½āµĆm=3£¬
”ąµćQ×ų±źĪŖ(3,4)£»
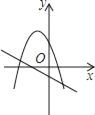
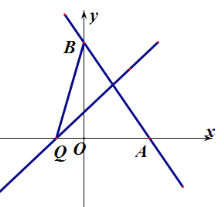
¢ŚČēĶ¼£¬µ±µćQĪ»ÓŚAB×ó²ąŹ±£¬QĒ”ŗĆĪ»ÓŚxÖįÉĻ£¬“ĖŹ±SABQ ![]() £¬
£¬
“ĖŹ±Q×ų±źĪŖ£Ø-1,0£©£»
×ŪÉĻĖłŹö£ŗČō /span>SABQ 6 £¬ Q µćµÄ×ų±źĪŖ(3,4)»ņ£Ø-1,0£©£»
£Ø3£©ČēĶ¼£¬½«”÷OABŃŲÖ±ĻßAB·ÕŪ£¬µĆµ½”÷NAB£¬½«”÷OCBŃŲÖ±ĻßBC·ÕŪ£¬µĆµ½”÷HCB£¬ŃÓ³¤HC”¢NA½»ÓŚµćE£¬ŌņĖıߊĪBHENĪŖÕż·½ŠĪ£¬ĒŅBN=BH=HE=NE=OB=4£¬NA=OA=2£¬AE=NE-AN=2£¬
ÉčOC=n£¬ŌņHC=n£¬CE=4-n£¬
ŌŚRt”÷ACEÖŠ£¬![]() £¬½āµĆ
£¬½āµĆ![]() £¬
£¬
ĖłŅŌµćC×ų±źĪŖ£Ø![]() £© £¬
£© £¬
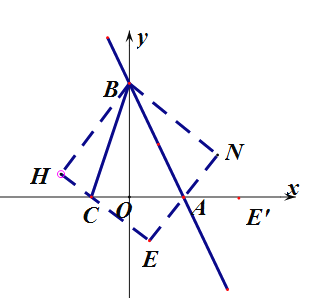
ČēĶ¼£ŗ”ßD µćŌŚÖ±ĻßÉĻ![]() ÉĻ£¬ŗį×ų±źĪŖ 1£¬
ÉĻ£¬ŗį×ų±źĪŖ 1£¬
”ąy=-2”Į1+4=2£¬
ĖłŅŌµćD×ų±źĪŖ£Ø![]() £©£»
£©£»
”߶Ƶć M µÄ×ų±źĪŖ£Øa£¬a£©£¬
”ąµćMŌŚÖ±Ļßy=xÉĻ£¬
ĖłŅŌµćC¹ŲÓŚÖ±Ļßy=x¶Ō³ĘµÄµćFµÄ×ų±źĪŖ£Ø![]() £©£¬
£©£¬
Į¬½ÓDF£¬ŌņDFĪŖCM+DMµÄ×īŠ”Öµ£»
×÷µćDG”ĶyÖį£¬“¹Ö±ĪŖG£¬
ŌŚRt”÷DGFÖŠ£¬DF=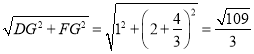 £»
£»
”ąCM+MD µÄ×īŠ”ÖµĪŖ![]() £®
£®

 æŖŠÄæģĄÖ¼ŁĘŚ×÷ŅµŹī¼Ł×÷ŅµĪ÷°²³ö°ęÉēĻµĮŠ“š°ø
æŖŠÄæģĄÖ¼ŁĘŚ×÷ŅµŹī¼Ł×÷ŅµĪ÷°²³ö°ęÉēĻµĮŠ“š°ø ĆūĢāѵĮ·ĻµĮŠ“š°ø
ĆūĢāѵĮ·ĻµĮŠ“š°ø