题目内容
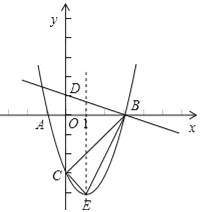
【题目】如图,抛物线![]() (a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线
(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线![]() 与y轴交于点D.
与y轴交于点D.
(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)证明见解析;(3)P(1,﹣1)或P(1,
;(2)证明见解析;(3)P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,
)或P(1,![]() )或P(1,
)或P(1,![]() ).
).
【解析】
试题分析:(1)先求出点C的坐标,在由BO=OC=3AO,确定出点B,A的坐标,最后用待定系数法求出抛物线解析式;
(2)先求出点A,B,C,D,E的坐标,从而求出BC,BE,CE,OD,OB,BD,求出比值,得到![]() 得出结论;
得出结论;
(3)设出点P的坐标,表示出PB,PC,求出BC,分三种情况计算即可.
试题解析:(1)∵抛物线![]() ,∴c=﹣3,∴C(0,﹣3),∴OC=3,∵BO=OC=3AO,∴BO=3,AO=1,∴B(3,0),A(﹣1,0),∵该抛物线与x轴交于A、B两点,∴
,∴c=﹣3,∴C(0,﹣3),∴OC=3,∵BO=OC=3AO,∴BO=3,AO=1,∴B(3,0),A(﹣1,0),∵该抛物线与x轴交于A、B两点,∴![]() ,∴
,∴![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)由(1)知,抛物线解析式为![]() =
=![]() ,∴E(1,﹣4),∵B(3,0),A(﹣1,0),C(0,﹣3),∴BC=
,∴E(1,﹣4),∵B(3,0),A(﹣1,0),C(0,﹣3),∴BC=![]() ,BE=
,BE=![]() ,CE=
,CE=![]() ,∵直线
,∵直线![]() 与y轴交于点D,∴D(0,1),∵B(3,0),∴OD=1,OB=3,BD=
与y轴交于点D,∴D(0,1),∵B(3,0),∴OD=1,OB=3,BD=![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,∴△BCE∽△BDO;
,∴△BCE∽△BDO;
(3)存在,理由:设P(1,m),∵B(3,0),C(0,﹣3),∴BC=![]() ,PB=
,PB=![]() ,PC=
,PC=![]() ,∵△PBC是等腰三角形,∴分三种情况讨论:
,∵△PBC是等腰三角形,∴分三种情况讨论:
①当PB=PC时,∴![]() =
=![]() ,∴m=﹣1,∴P(1,﹣1);
,∴m=﹣1,∴P(1,﹣1);
②当PB=BC时,∴![]() =
=![]() ,∴m=
,∴m=![]() ,∴P(1,
,∴P(1,![]() )或P(1,﹣
)或P(1,﹣![]() );
);
③当PC=BC时,∴![]() =
=![]() ,∴m=
,∴m=![]() ,∴P(1,
,∴P(1,![]() )或P(1,
)或P(1,![]() );
);
综上所述:符合条件的P点坐标为P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,
)或P(1,![]() )或P(1,
)或P(1,![]() ).
).



