题目内容
如图,A、B分别是x轴和y轴上的点,以AB为直径作⊙M,过M点作AB的垂线交⊙M于点C,C在双曲线y=
(x<0)上,若OA-OB=4,则k的值是 .

【答案】分析:作CD⊥x轴于D,CE⊥y轴于E,连结AC、BC,由AB为⊙M的直径,根据圆周角定理的推论得到∠ACB=90°,而CM⊥AB,则△ACB为等腰直角三角形,可得到CA=CB,AB= BC,再根据圆周角定理得到∠CAO=∠CBO,易证得Rt△ACD≌Rt△BCE,则CD=CE,于是可设C点坐标为(-t,t),A点坐标为(a,0),B点坐标为(0,b),由OA-OB=4,则a=b-4,得到a2=(b-4)2=b2-8b+16①,再利用勾股定理有AB2=a2+b2,BC2=CE2+BE2,则
BC,再根据圆周角定理得到∠CAO=∠CBO,易证得Rt△ACD≌Rt△BCE,则CD=CE,于是可设C点坐标为(-t,t),A点坐标为(a,0),B点坐标为(0,b),由OA-OB=4,则a=b-4,得到a2=(b-4)2=b2-8b+16①,再利用勾股定理有AB2=a2+b2,BC2=CE2+BE2,则 (a2+b2)=t2+(t-b)2②,由①②得t2-4-bt+2b=0,分解变形后可解得t=2,然后把C点坐标代入反比例函数解析式可求出k的值.
(a2+b2)=t2+(t-b)2②,由①②得t2-4-bt+2b=0,分解变形后可解得t=2,然后把C点坐标代入反比例函数解析式可求出k的值.
解答:解:作CD⊥x轴于D,CE⊥y轴于E,连结AC、BC,如图,
∵AB为⊙M的直径,
∴∠ACB=90°,
又∵CM⊥AB,
∴△ACB为等腰直角三角形,
∴CA=CB,AB= BC,
BC,
∵∠CAO=∠CBO,
∵在△ACD和△BCE中
 ,
,
∴△ACD≌△BCE(AAS),
∴CD=CE,
设C点坐标为(-t,t),A点坐标为(a,0),B点坐标为(0,b),
∵OA-OB=4,即-a-(-b)=4,
∴a=b-4,
∴a2=(b-4)2=b2-8b+16①,
∵AB2=a2+b2,BC2=CE2+BE2,
∴ (a2+b2)=t2+(t-b)2②,
(a2+b2)=t2+(t-b)2②,
由①②得t2-4-bt+2b=0,
∴(t+2)(t-2)-b(t-2)=0,
∴(t-2)(t+2-b)=0,
而t+2-b≠0,
∴t-2=0,解得t=2,
∴C点坐标为(-2,2),
把C(-2,2)代入y= 得k=-2×2=-4.
得k=-2×2=-4.
故答案为-4.
点评:本题考查了反比例函数的综合题:点在反比例函数图象上,则点的坐标满足其解析式;熟练掌握圆周角定理;会运用三角形全等和等腰直角三角形的性质得到线段之间的关系,利用勾股定理建立等量关系.
 BC,再根据圆周角定理得到∠CAO=∠CBO,易证得Rt△ACD≌Rt△BCE,则CD=CE,于是可设C点坐标为(-t,t),A点坐标为(a,0),B点坐标为(0,b),由OA-OB=4,则a=b-4,得到a2=(b-4)2=b2-8b+16①,再利用勾股定理有AB2=a2+b2,BC2=CE2+BE2,则
BC,再根据圆周角定理得到∠CAO=∠CBO,易证得Rt△ACD≌Rt△BCE,则CD=CE,于是可设C点坐标为(-t,t),A点坐标为(a,0),B点坐标为(0,b),由OA-OB=4,则a=b-4,得到a2=(b-4)2=b2-8b+16①,再利用勾股定理有AB2=a2+b2,BC2=CE2+BE2,则 (a2+b2)=t2+(t-b)2②,由①②得t2-4-bt+2b=0,分解变形后可解得t=2,然后把C点坐标代入反比例函数解析式可求出k的值.
(a2+b2)=t2+(t-b)2②,由①②得t2-4-bt+2b=0,分解变形后可解得t=2,然后把C点坐标代入反比例函数解析式可求出k的值.解答:解:作CD⊥x轴于D,CE⊥y轴于E,连结AC、BC,如图,

∵AB为⊙M的直径,
∴∠ACB=90°,
又∵CM⊥AB,
∴△ACB为等腰直角三角形,
∴CA=CB,AB=
 BC,
BC,∵∠CAO=∠CBO,
∵在△ACD和△BCE中
 ,
,∴△ACD≌△BCE(AAS),
∴CD=CE,
设C点坐标为(-t,t),A点坐标为(a,0),B点坐标为(0,b),
∵OA-OB=4,即-a-(-b)=4,
∴a=b-4,
∴a2=(b-4)2=b2-8b+16①,
∵AB2=a2+b2,BC2=CE2+BE2,
∴
 (a2+b2)=t2+(t-b)2②,
(a2+b2)=t2+(t-b)2②,由①②得t2-4-bt+2b=0,
∴(t+2)(t-2)-b(t-2)=0,
∴(t-2)(t+2-b)=0,
而t+2-b≠0,
∴t-2=0,解得t=2,
∴C点坐标为(-2,2),
把C(-2,2)代入y=
 得k=-2×2=-4.
得k=-2×2=-4.故答案为-4.
点评:本题考查了反比例函数的综合题:点在反比例函数图象上,则点的坐标满足其解析式;熟练掌握圆周角定理;会运用三角形全等和等腰直角三角形的性质得到线段之间的关系,利用勾股定理建立等量关系.

练习册系列答案
相关题目

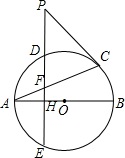 如图:AB、AC分别是⊙O的直径和弦,D为弧AC上一点,DE⊥AB于点H,交⊙O于点E,交AC于点F.P为ED延长线上一点,连PC.
如图:AB、AC分别是⊙O的直径和弦,D为弧AC上一点,DE⊥AB于点H,交⊙O于点E,交AC于点F.P为ED延长线上一点,连PC. 如图,AB和AC分别是⊙O的直径和弦,OD⊥AC于D点,若OA=4,∠A=30°,则BD等于( )
如图,AB和AC分别是⊙O的直径和弦,OD⊥AC于D点,若OA=4,∠A=30°,则BD等于( ) 已知:如图,E、F分别是正方形ABCD边BC、AD上的点,且BE=DF
已知:如图,E、F分别是正方形ABCD边BC、AD上的点,且BE=DF 桌上放着一个圆柱和一个长方体,如图(1),请说出下列三幅图(如图(2))分别是从哪个方向看到的.
桌上放着一个圆柱和一个长方体,如图(1),请说出下列三幅图(如图(2))分别是从哪个方向看到的.