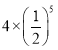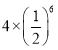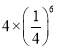Question

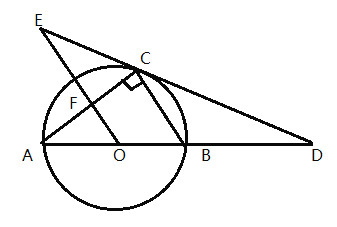
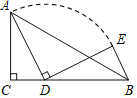
【题目】如图,在△ACD中,∠ACD＝90°,AC＝b,CD＝a,AD＝c,点B在CD的延长线上

(1)求证:关于x的一元二次方程必有实数根

(2)当b＝3,CB＝5时.将线段AD绕点D顺时针旋转90°,得到线段DE,连接BE,则当a的值为多少时,线段BE的长最短,最短长度是多少？

Answer 1

【答案】（1）见解析；（2）当a=1时，线段BE最短，最短长度是

【解析】

（1）根据勾股定理得到，代入一元二次方程根的判别式得，即可得证；

（2）过E作EF⊥BC于F，根据余角的性质得到∠DEF=∠ADC，根据全等三角形的性质得到DF=AC=b=3，EF=CD，设CD=x，则，于是得出结论.

（1）证明： 在Rt△ACD中，由勾股定理得：，即

∴关于x的一元二次方程必有实数根

（2）过E作EF⊥BC于F，如图

∵∠C=∠ADE=90°

∴∠EFD=∠C=90°，∠FED+∠EDF=90°，∠EDF+∠ADC=90°

∴∠DEF=∠ADC

在△EDF和△DAC中

∴△EDF≌△DAC（AAS）

∴DF=AC=b=3，EF=CD

设CD=x，则

∴的最小值是2

∴当CD=1时，BE的最小值是

即当a=1时，线段BE最短，最短长度是