题目内容
如图,⊙O的半径为2,弦AB=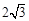 ,点C在弦AB上,
,点C在弦AB上, ,则OC的长为( )
,则OC的长为( )

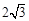 ,点C在弦AB上,
,点C在弦AB上, ,则OC的长为( )
,则OC的长为( )
A. | B. | C. | D. |
D.
试题分析:首先过点O作OD⊥AB于点D,由垂径定理,即可求得AD,BD的长,然后由勾股定理,可求得OD的长,然后在Rt△OCD中,利用勾股定理即可求得OC的长.
过点O作OD⊥AB于点D,

∵AB=2
 ,
,∴AD=BD=
 AB=
AB= ,AC=
,AC= AB=
AB= ,
,∴CD=AD-AC=
 ,
,∵⊙O的半径为2,
即OB=2,
∴在Rt△OBD中,OD=
 ,
,在Rt△OCD中,OC=
 .
.故选D.
考点: 1.垂径定理;2.勾股定理.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目





 cm
cm cm
cm cm
cm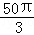 cm
cm


