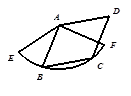题目内容
已知梯形ABCD内接于⊙O,AB//CD,AB="8" cm,CD ="6" cm,⊙O的半径为5cm,则S梯形ABCD=
49cm2或7cm2
过O作OE⊥CD于E,交AB于F.连接OA,OC.
在直角△OCE中,CE= CD=1,OC=4.
CD=1,OC=4.
∴OE= =4;
=4;
同理,在直角△AOF中,AF= AB=4.
AB=4.
∴OF= =3.
=3.
1)当CD与AB在圆心的同侧时,
则梯形的高EF=1.
则梯形的面积是: (CD+AB)•EF=
(CD+AB)•EF=  ×(6+8)×1=7cm2;
×(6+8)×1=7cm2;
2)当CD与AB在圆心的两侧时,
梯形的高EF=7.
则梯形的面积是: (CD+AB)•EF=
(CD+AB)•EF=  ×(8+6)×7=49cm2.
×(8+6)×7=49cm2.
故答案是:49cm2或7cm2

在直角△OCE中,CE=
 CD=1,OC=4.
CD=1,OC=4.∴OE=
 =4;
=4;同理,在直角△AOF中,AF=
 AB=4.
AB=4.∴OF=
 =3.
=3.1)当CD与AB在圆心的同侧时,
则梯形的高EF=1.
则梯形的面积是:
 (CD+AB)•EF=
(CD+AB)•EF=  ×(6+8)×1=7cm2;
×(6+8)×1=7cm2;2)当CD与AB在圆心的两侧时,
梯形的高EF=7.
则梯形的面积是:
 (CD+AB)•EF=
(CD+AB)•EF=  ×(8+6)×7=49cm2.
×(8+6)×7=49cm2.故答案是:49cm2或7cm2

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
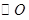 上,若
上,若 那么
那么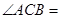 .
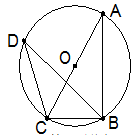
. 

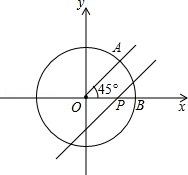
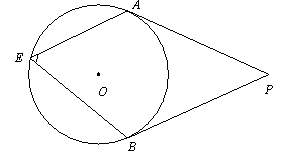
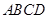 的两个顶点
的两个顶点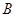 、
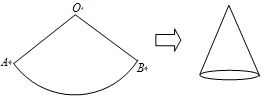
、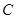 恰好落在扇形
恰好落在扇形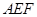 的
的 上时,
上时,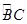 的长度等于 (结果保留
的长度等于 (结果保留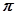 ).
).