题目内容
在围棋盒中有x枚黑色棋子和y枚白色棋子,从盒中随机取一枚棋子,如果它是黑色棋子的概率为
,则y与x的函数关系式可以表示为( )
| 4 |
| 9 |
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
分析:根据围棋盒中有x颗黑色棋子和y颗白色棋子,故棋子的总个数为x+y,再根据黑色棋子的概率公式列式解答即可.
解答:解:∵围棋盒中有x颗黑色棋子和y颗白色棋子,
∴棋子的总个数为x+y,
∵从中随机摸出一个棋子,
摸到黑色棋子的概率为
,
∴
=
,
解得,y=
x.
故选D.
∴棋子的总个数为x+y,
∵从中随机摸出一个棋子,
摸到黑色棋子的概率为
| 4 |
| 9 |
∴
| x |
| x+y |
| 4 |
| 9 |
解得,y=
| 5 |
| 4 |
故选D.
点评:本题考查的是根据实际问题列一次函数关系式及随机事件概率的求法.关键是掌握如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 ,则y与x的函数关系式可以表示为
,则y与x的函数关系式可以表示为


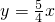
 ,则y与x的函数关系式可以表示为( )
,则y与x的函数关系式可以表示为( )


