题目内容
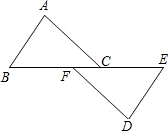如图：点B，E，C，F在一条直线上，FB=CE，AB∥ED，AC∥DF．求证：AB=DE，AC=DF．
证明：∵FB=EC，
∴BC=EF，
又∵AB∥ED，AC∥DF，
∴∠B=∠E，∠ACB=∠DFE，
在△ABC与△DEF中，
∵
∴△ABC≌△DEF（ASA），
∴AB=DE，AC=DF．
分析：结合已知条件可由ASA得出△ABC≌△DEF，进而可得出结论．
点评：本题主要考查了全等三角形的判定及性质问题，应熟练掌握．
∴BC=EF，
又∵AB∥ED，AC∥DF，
∴∠B=∠E，∠ACB=∠DFE，
在△ABC与△DEF中，
∵
∴△ABC≌△DEF（ASA），
∴AB=DE，AC=DF．
分析：结合已知条件可由ASA得出△ABC≌△DEF，进而可得出结论．
点评：本题主要考查了全等三角形的判定及性质问题，应熟练掌握．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
BE、CD、CE，已知∠BED=30°．
如图，点A的坐标为（2| 2 |
| A、（0，0） | ||||||||
B、(
| ||||||||
| C、（1，1） | ||||||||
D、(
|
12、如图，点O到直线l的距离为3，如果以点O为圆心的圆上只有两点到直线l的距离为1，则该圆的半径r的取值范围是