题目内容
按要求解下列方程组.
(1) (用代入法);
(用代入法);
(2) (用加减法).
(用加减法).
解:(1)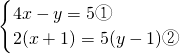 ,
,
由①,得y=4x-5 ③,
把③代入②,得2(x+1)=5(4x-5-1),
解得x= .
.
把x= 代入③,得y=4×
代入③,得y=4× -5=
-5=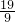 .
.
所以原方程组的解是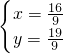 .
.
(2)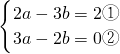 ,
,
①×3,得6a-9b=6 ③,
②×2,得6a-4b=0 ④,
④-③,得5b=-6,
解得b=- .
.
把b=- 代入②,得3a-2×(-
代入②,得3a-2×(- )=0,
)=0,
解得a=- .
.
所以原方程组的解是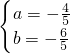 .
.
分析:(1)由于方程①中未知数y的系数的绝对值是1,先用含x的代数式表示y,再把它代入方程②,即可消去y,求出x的值,然后代入求y的值;
(2)先求出x或y的最小公倍数,将方程中的某个未知数的系数变成其最小公倍数以后,再相减消元.
点评:本题考查了二元一次方程组的解法.解二元一次方程组的基本思想是消元,消元的方法有代入法和加减法.如果题目没有明确指出运用什么方法解方程组,那么需要根据方程组的特点灵活选用解法.一般说来,当方程组中有一个方程的未知数的系数的绝对值是1或常数项是0时,运用代入法求解,除此之外,选用加减法求解,将会使计算较为简便.
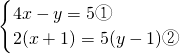 ,
,由①,得y=4x-5 ③,
把③代入②,得2(x+1)=5(4x-5-1),
解得x=
 .
.把x=
 代入③,得y=4×
代入③,得y=4× -5=
-5=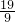 .
.所以原方程组的解是
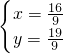 .
.(2)
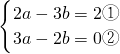 ,
,①×3,得6a-9b=6 ③,
②×2,得6a-4b=0 ④,
④-③,得5b=-6,
解得b=-
 .
.把b=-
 代入②,得3a-2×(-
代入②,得3a-2×(- )=0,
)=0,解得a=-
 .
.所以原方程组的解是
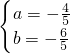 .
.分析:(1)由于方程①中未知数y的系数的绝对值是1,先用含x的代数式表示y,再把它代入方程②,即可消去y,求出x的值,然后代入求y的值;
(2)先求出x或y的最小公倍数,将方程中的某个未知数的系数变成其最小公倍数以后,再相减消元.
点评:本题考查了二元一次方程组的解法.解二元一次方程组的基本思想是消元,消元的方法有代入法和加减法.如果题目没有明确指出运用什么方法解方程组,那么需要根据方程组的特点灵活选用解法.一般说来,当方程组中有一个方程的未知数的系数的绝对值是1或常数项是0时,运用代入法求解,除此之外,选用加减法求解,将会使计算较为简便.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 (用代入消元法)
(用代入消元法) ,(用加减消元法)
,(用加减消元法) (用代入消元法)
(用代入消元法) ,(用加减消元法)
,(用加减消元法) (用代入法);
(用代入法); (用加减法).
(用加减法).