Question

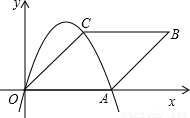
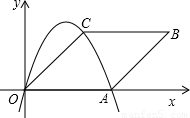
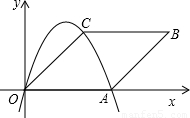
如图，菱形OABC放在平面直角坐标系内，点A在x轴的正半轴上，点B在第一象限，其坐标为（8，4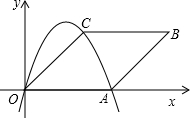）．抛物线y=ax²+bx+c过点O、A、C．
（1）求抛物线的解析式；
（2）将菱形向左平移，设抛物线与线段AB的交点为D，连接CD．
①当点C又在抛物线上时求点D的坐标；
②当△BCD是直角三角形时，求菱形的平移的距离．

Answer 1

分析：（1）过B作BE⊥OA于E，则可知OE=8，设菱形的边长是a，则AE=8-a，在直角△ABE中，根据勾股定理，就可以得到关于边长的方程，求出边长．则点O、A、C的坐标就可以求出．根据待定系数法就可以解得抛物线的解析式；
（2）①当点C又在抛物线上时，C点的坐标与原来的点的纵坐标相同，把y=4代入抛物线的解析式，就可以求出C点移动前后的坐标，A，B两点移动情况相同，因而A，B两点的移动后坐标可以求出，根据待定系数法就可以求出函数解析式，把这个解析式与抛物线的解析式组成方程组就可以求出D的坐标．
②当△BCD是直角三角形时点D到BC的距离可以求出，得到点D的纵坐标，代入抛物线的解析式就可以得到方程，解方程就可以求出D的坐标，得到菱形的平移的距离．

解答：解：（1）过B作BE⊥OA于E，过C作CF⊥OA于F

由B（8，4），菱形OABC
可得AB+AE=OA+AE=8，BE=4
又因为AE²+BE²=AB²
解得AO=AB=5（2分）
∴A（5，0）
∵OC=5，CF=BE=4，
由勾股定理得OF=3．
∴C（3，4）．
所以过O、A、C三点的抛物线解析式是y=-

2

3

x2+

10

3

x（2分）；

（2）①当y=4时，-

2

3

x2+

10

3

x=4
解得x₁=3（舍去），x₂=2（1分）．
所以菱形向左平移了1个单位长度直线AB也向左平移了1个单位长度
原直线AB为：y=

4

3

x-

20

3

则平移后的直线为y=

4

3

(x+1)-

20

3

=

4

3

x-

16

3

（1分）
此时点D的坐标为方程组

y=- 2 3 x2+ 10 3 x y= 4 3 x- 16 3

的解（1分）
可得点D坐标为（

3+ 41

2

，

2 41 -10

3

）（1分）．
（点（

3- 41

2

，

-2 41 -10

3

）不合题意舍去）
②作CD⊥AB于D，作DH⊥BC于H，
则CD=CF=4，在直角△BCD中，BD=

BC2-CD2

=3，
则DH=

CD•CB

BC

=

12

5

，
当△BCD是直角三角形时，则点D到BC的距离是

12

5

，则点D的纵坐标为4-

12

5

=

8

5

当y=

8

5

时-

2

3

x2+

10

3

x=

8

5

解得x1=

25+ 385

10

x2=

25- 385

10

原直线AB：y=

4

3

x-

20

3

上有一点（

31

5

，

8

5

）
所以菱形移动的距离为

37± 385

10

每对一个得（2分）．

点评：本题主要考查了待定系数法求函数的解析式．注意数与形的结合是解决本题的关键．