Question

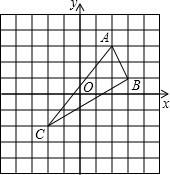
如图，已知△ABC：
（1）AC的长等于______；
（2）若将△ABC向右平移2个单位得到△A′B′C′，则A点的对应点A′的坐标是______；
（3）若将△ABC绕点C按顺时针方向旋转90°后得到△A₁B₁C₁，则A点对应点A₁的坐标是______；
（4）在图中画出第（2）问中△A′B′C′或第（3）问中△A₁B₁C₁的图形．

Answer 1

解：（1）由图形可知：A（-1，2），C（0，-1），
由勾股定理得：AC==，
故答案为：．

（2）A（-1，2），
∵将△ABC向右平移2个单位得到△A′B′C′，
∴-1+2=1，
∴A点的对应点A′的坐标是（1，2），
故答案为：（1，2）．

（3）根据图形旋转，A₁落在X轴上，且AC=CA₁=，
∵OC=1，
∴OA₁=3，
∴A₁（3，0），
故答案为：（3，0）．

（4）如图：△A′B′C′或△A₁B₁C₁，
∴△A′B′C′或△A₁B₁C₁即为所求作的图形．

分析：（1）由图形可知：A（-1，2），C（0，-1），根据勾股定理求出AC即可；
（2）根据A（-1，2）和平移的性质得到-1+2=1，即可求出A点的对应点A′的坐标；
（3）根据作图-旋转变换得到A₁落在X轴上，且AC=CA₁=，根据OC=1，求出OA₁=3，即可得到答案；
（4）根据平移的性质和旋转变换的性质，根据△ABC的顶点的坐标特点求出对应点的坐标，画出即可．
点评：本题主要考查对勾股定理，作图-平移变换的性质，作图-旋转变换的性质等知识点的理解和掌握，能根据性质正确画图是解此题的关键，题型较好，比较典型．