题目内容
已知等腰△ABC的外心是O，AB=AC，∠BOC=100°，则∠ABC=________．
25°或65°
分析：画出相应图形，分△ABC为锐角三角形和钝角三角形2种情况解答即可．
解答：
解：
（1）圆心O在△ABC外部，
在优弧BC上任选一点D，连接BD，CD．
∴∠BDC=
∠BOC=50°，
∴∠BAC=180°-∠BDC=130°；
∵AB=AC，
∴∠ABC=（180°-∠BAC）÷2=25°；
（2）圆心O在△ABC内部．
∠BAC=∠BOC=50°，
∵AB=AC，
∴∠ABC=（180°-∠BAC）÷2=65°；
故答案为25°或65°．
点评：主要考查三角形圆周角定理及等腰三角形的性质；分情况探讨是解决本题的易错点；用到的知识点为：同弧所对的圆周角等于圆心角的一半；圆内接四边形的对角互补．
分析：画出相应图形，分△ABC为锐角三角形和钝角三角形2种情况解答即可．
解答：
解：（1）圆心O在△ABC外部，
在优弧BC上任选一点D，连接BD，CD．
∴∠BDC=
∠BOC=50°，∴∠BAC=180°-∠BDC=130°；
∵AB=AC，
∴∠ABC=（180°-∠BAC）÷2=25°；
（2）圆心O在△ABC内部．
∠BAC=∠BOC=50°，∵AB=AC，
∴∠ABC=（180°-∠BAC）÷2=65°；
故答案为25°或65°．
点评：主要考查三角形圆周角定理及等腰三角形的性质；分情况探讨是解决本题的易错点；用到的知识点为：同弧所对的圆周角等于圆心角的一半；圆内接四边形的对角互补．
练习册系列答案
相关题目
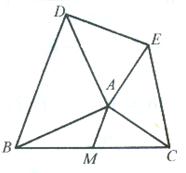12、如图，已知在△ABC外作等腰直角三角形ABD和等腰直角三角形ACE，且∠BAD=∠CAE=90°，AM为△ABC中BC边上的中线，连接DE．求证：DE=2AM．
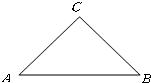13、已知等腰Rt△ABC（如图），试取斜边AB上的一点为圆心画图，使点A，B，C分别在所画的圆内、圆外和圆上．
