Question

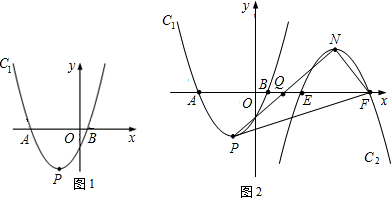
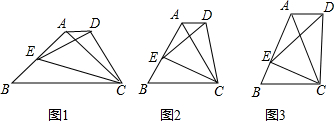
如图①所示，将一个正三角形纸片沿着它的一条边上的高剪开，得到如图②所示的两个全等的Rt△ABC、Rt△DEF．

(1)根据正三角形的性质可知：在图②中，∠ABC＝∠DEF＝30°，AB＝DE＝2AC＝2DF．由此请你归纳一下在含30°角的直角三角形中，30°角所对的直角边与斜边之间的关系：

在含30°角的直角三角形中，30°角所对的直角边________；

(2)将这两个直角三角形纸片按如图③放置，使点B、D重合，点F在BC上．固定纸片DEF，将△ABC绕点F逆时针旋转角α(0°＜α＜90°)，使四边形ACDE为以ED为底的梯形(如图④所示)，求此时α的值；

(3)猜想图④中AE与CD之间的大小关系，并说明理由．

Answer 1

答案：
解析：

(1)等于斜边的一半．　3分 　　(2)α＝30°．　6分 　　(3)法一：在图④中，设DE交BC于点I，作AH垂直于ED设FD＝2x，则由(1)得ED＝4x，BD＝x，又因为AC＝FD＝2x，所以HI＝2x，则EH＝4x－2x－x＝x，因为AC∥DE，所以AH＝CI，易得ΔAHE≌ΔCID，所以AE＝CD　12分 　　法二：如图⑤所示，取DE的中点G，连接CG、AG． 　　则不难得到AG＝CD，CG＝AE，设DE交BC于点I． 　　又CB⊥DG，DG＝DF＝2BI，故I为DG中点． 　　由垂直平分线的性质知：CD＝CG＝AE　12分