Question

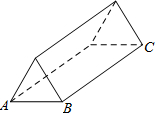一个蔬菜大棚（四周都是塑料薄膜）的形状如图．
（1）它可以看成是怎样的棱柱？
（2）若它的底面是边长为AB=3米的正三角形，大棚总长BC=10米，那么搭建这个蔬菜大棚需要多少的塑料薄膜？

Answer 1

分析：（1）利用已知图形直接可以得出它可以看成是直三棱柱；
（2）根据等边三角的性质得出BE，DE的长度，进而再求出侧面积即可得出答案．

解答：解：（1）根据图形它可以看成是直三棱柱；

（2）如图，作DE⊥AB于点E，根据题意可得出：AE=BE=

3

2

，
AB=BD=AD=3，
则DE=

32-( 3 2 )2

=

3 3

2

，
故S_底=

1

2

×AB×DE=

1

2

×

3 3

2

×3=

9 3

4

，
S_侧=3×10=30，
S=2S_底+2S_侧=60+

9 3

4

×2=60+

9 3

2

．
答：搭建这个蔬菜大棚需要60+

9 3

2

平方米的塑料薄膜．

点评：此题主要考查了几何体的表面积以及等边三角形的性质等知识，根据已知得出蔬菜大棚各组成部分面积是解题关键．