题目内容
2.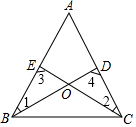 如图,在△ABC中,D,E分别是AC,AB上的点,BD与CE交于点O,给出下列三个条件:①∠1=∠2;②∠3=∠4;③BE=CD.
如图,在△ABC中,D,E分别是AC,AB上的点,BD与CE交于点O,给出下列三个条件:①∠1=∠2;②∠3=∠4;③BE=CD.(1)上述三个条件中,哪两个条件可判定△ABC是等腰三角形;(用序号写出所有情形)
(2)选择第(1)小题中的一种情况,证明△ABC是等腰三角形.
分析 (1)根据全等三角形的判定性质,可得OB与OC的关系,根据等腰三角形的性质,可得∠OBC与∠OCB的关系,根据等腰三角形的判定,可得答案;
(2)根据AAS,可得OB与OC的关系,根据等腰三角形的性质,可得∠OBC与∠OCB的关系,根据等腰三角形的判定,可得答案.
解答 解:(1)由①③和②③都可以判定△ABC是等腰三角形;
(2)选择①③,证明如下:
证明:在△BOE和△COD中,
$\left\{\begin{array}{l}{∠1=∠2}\\{∠BOE=∠COD}\\{BE=CD}\end{array}\right.$,
∴△BOE≌△COD(AAS),
∴BO=CD(全等三角形的对应边相等),
∴∠OBC=∠OCB(等腰三角形的两底角相等).
∵∠1+∠OBC=∠2+∠OCB(等式的性质),
即∠ABC=∠ACB,
∴AB=AC(等角对等边),
即△ABC是等腰三角形.
选择②③时,证明如下:
证明:在△BOE和△COD中,
$\left\{\begin{array}{l}{∠3=∠4}\\{∠BOE=∠COD}\\{BE=CD}\end{array}\right.$,
∴△BOE≌△COD(AAS),
∴∠1=∠2(全等三角形的对应角相等),
∴BO=CD(全等三角形的对应边相等),
∴∠OBC=∠OCB(等腰三角形的两底角相等).
∵∠1+∠OBC=∠2+∠OCB(等式的性质),
即∠ABC=∠ACB,
∴AB=AC(等角对等边),
即△ABC是等腰三角形.
点评 本题考查了等要三角形的判定,利用全等三角形的判定性质得出OB与OC的关系是解题关键,又利用了等腰三角形的性质与判定.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
7.一个三角形的两边长分别为3cm和8cm,则此三角形第三边长可能是( )
| A. | 3cm | B. | 5cm | C. | 7cm | D. | 11cm |
11. 下面圆柱体的侧面积为( )
下面圆柱体的侧面积为( )
 下面圆柱体的侧面积为( )
下面圆柱体的侧面积为( )| A. | 31.4 | B. | 62.8 | C. | 39.25 | D. | 15.7 |
4.在科技迅猛发展的今天,移动电话成为了人们生活中非常普及的通讯工具,选择经济实惠的计费方式成为了人们所关心的具有实际意义的问题.下表是两种移动电话的计费方式:
若小明的爸爸每月打电话的时间在300分钟,请问选择哪种方式省钱( )
| 月使用费(元) | 主叫限定时间(分钟) | 主叫超时费/(元/分) | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免费 |
| 方式二 | 88 | 350 | 0.19 | 免费 |
| A. | 方式一 | B. | 方式二 | C. | 两种方式一样 | D. | 无法确定 |
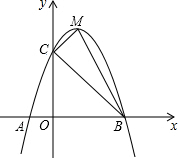 如图,抛物线y=ax2+bx+c交x轴于A(-1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点.
如图,抛物线y=ax2+bx+c交x轴于A(-1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点.