题目内容
 在等腰梯形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以每秒2个单位长度的速度沿AD→DC向终点C运动,同时点Q从点B出发,以每秒1个单位的速度沿BA向终点A运动,设运动时间为t秒.
在等腰梯形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以每秒2个单位长度的速度沿AD→DC向终点C运动,同时点Q从点B出发,以每秒1个单位的速度沿BA向终点A运动,设运动时间为t秒.(1)当t为何值时,四边形PQBC为平行四边形时?
(2)在整个运动过程中,当t为何值时,以点C、P、Q为顶点的三角形是直角三角形?
分析:(1)根据对边平行且相等的四边形是平行四边形,求出PC=BQ就可得到答案.
(2)有两种情况,根据勾股定理逆定理可求出边长,进而求出时间.
(2)有两种情况,根据勾股定理逆定理可求出边长,进而求出时间.
解答:解:(1)当点P在AD边上时,PC与BQ不平行,
故此时四边形PQBC不可能为平行四边形;
当点P在DC边上时,如图1.
PC=12-2t,BQ=t,
∵四边形PQBC为平行四边形,
∴PC=BQ.
∴12-2t=t,t=4.
∴当t=4时,四边形PQBC为平行四边形.

(2)作高DE、CF,易求高DE=CF=4,
当t<
时,点P在AD上,只有当CP垂直于CQ时以点C、P、Q为顶点的三角形是直角三角形
这时CQ2=42+(3-t)2=t2-6t+25,
PQ2=(
×4)2+(13-t-
×3)2=
-
+169,
CP2=(4-
×4)2+(13-3-
×3)2=4t2-
+116,
由CP2+CQ2=PQ2得4t2-
+116+t2-6t+25=
-
+169无解
当t≥
时,点P在DC上,显然点Q运动到点F处(此时t=3)
当PQ垂直于AB时,
此时5+7-2t=t-3,
解得:t=5
当PQ垂直于CQ时以点C、P、Q为顶点的三角形是直角三角形(此时无解)
综上可知,当t=3秒或5秒时点C、P、Q为顶点的三角形是直角三角形.
故此时四边形PQBC不可能为平行四边形;
当点P在DC边上时,如图1.
PC=12-2t,BQ=t,
∵四边形PQBC为平行四边形,
∴PC=BQ.
∴12-2t=t,t=4.
∴当t=4时,四边形PQBC为平行四边形.

(2)作高DE、CF,易求高DE=CF=4,
当t<
| 5 |
| 2 |
这时CQ2=42+(3-t)2=t2-6t+25,
PQ2=(
| 2t |
| 5 |
| 2t |
| 5 |
| 185t2 |
| 25 |
| 286t |
| 5 |
CP2=(4-
| 2t |
| 5 |
| 2t |
| 5 |
| 184t |
| 5 |
由CP2+CQ2=PQ2得4t2-
| 184t |
| 5 |
| 185t2 |
| 25 |
| 286t |
| 5 |
当t≥
| 5 |
| 2 |
当PQ垂直于AB时,
此时5+7-2t=t-3,
解得:t=5
当PQ垂直于CQ时以点C、P、Q为顶点的三角形是直角三角形(此时无解)
综上可知,当t=3秒或5秒时点C、P、Q为顶点的三角形是直角三角形.
点评:本题考查等腰梯形的性质,平行四边形的判定和直角三角形的性质,熟记这些性质和判定进行求解.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.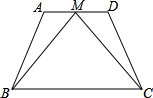 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.