题目内容
2010年5月“国际保护鲸鱼组织”准备派遣三艘护卫船在南极进行阻止“日本捕鲸船”的“护鲸行动”.在雷达显示图上,标明了三艘护卫船的坐标为O(0,0)、B(8,0)、C(8,6), 三艘护卫船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).
三艘护卫船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).(1)某时刻海面上出现一艘日本捕鲸船A,在护卫船C测得点A位于东南方向上,同时在护卫船B测得A位于北偏东60°方向上,求护卫船B到捕鲸船A的距离;
(2)若在三艘护卫船组成的△OBC区域内恰好没有探测盲点,求雷达的有效探测半径r.
分析:(1)作出点A的位置,过点A作AD⊥BC于点D,设CD=x,则BD=6-x,在RT△ABD中可求出x的值,进而可得出答案.
(2)恰好没有探测盲点,则三个圆相交于一点,这个点到三顶点的距离相等.
(2)恰好没有探测盲点,则三个圆相交于一点,这个点到三顶点的距离相等.
解答: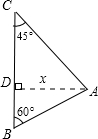 解:(1)如图,作出点A的位置,由题意得,BC=6,∠C=45°,∠B=60°,
解:(1)如图,作出点A的位置,由题意得,BC=6,∠C=45°,∠B=60°,
过点A作AD⊥BC于点D,设CD=x,则BD=6-x,
易知AD=CD=x,在Rt△ABD中,tan60°=
,
∴x=9-3
.
∴易求AB=6
-6.
(2)如图:若在三艘护卫船组成的△OBC区域内恰好没有探测盲点,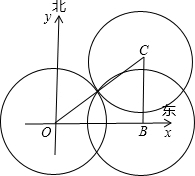
三个圆相交于一点,这个点到三顶点的距离相等,
∴r=
OC=
×
=5.
 解:(1)如图,作出点A的位置,由题意得,BC=6,∠C=45°,∠B=60°,
解:(1)如图,作出点A的位置,由题意得,BC=6,∠C=45°,∠B=60°,过点A作AD⊥BC于点D,设CD=x,则BD=6-x,
易知AD=CD=x,在Rt△ABD中,tan60°=
| AD |
| BD |
∴x=9-3
| 3 |
∴易求AB=6
| 3 |
(2)如图:若在三艘护卫船组成的△OBC区域内恰好没有探测盲点,

三个圆相交于一点,这个点到三顶点的距离相等,
∴r=
| 1 |
| 2 |
| 1 |
| 2 |
| 62+82 |
点评:本题考查了解直角三角形的应用,题出的比较新颖,难度一般,在解直角三角形的时候注意利用含有已知线段的直角三角形,这样能使问题简单化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 三艘护卫船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).
三艘护卫船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).