Question

8．如图，AD是△ABC的角平分线，DF⊥AB，垂足为点F，DE=DG．若△ADG和△AED的面积分别为50和30，则△EDF的面积为7.5．

Answer 1

分析 过点D作DH⊥AC于H，根据角平分线上的点到角的两边距离相等可得DF=DH，然后利用“HL”证明Rt△DEF和Rt△DGH全等，根据全等三角形的面积相等可得S_△EDF=S_△GDH，设面积为S，然后根据S_△ADF=S_△ADH列出方程求解即可．

解答 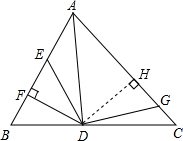解：如图，过点D作DH⊥AC于H，
∵AD是△ABC的角平分线，DF⊥AB，
∴DF=DH，
在Rt△DEF和Rt△DGH中，$\left\{\begin{array}{l}{DE=DG}\\{DF=DH}\end{array}\right.$，
∴Rt△DEF≌Rt△DGH（HL），
∴S_△EDF=S_△GDH，设面积为S，
同理Rt△ADF≌Rt△ADH，
∴S_△ADF=S_△ADH，
即30+S=50-S，
解得S=10．
故答案为10．

点评 本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，作辅助线构造出全等三角形并利用角平分线的性质是解题的关键．