题目内容
如图,已知点A(0,6),B(4,-2),C(7, ),过点B作x轴的垂线,交直线AC于点E,点F与点E关于点B对称.
),过点B作x轴的垂线,交直线AC于点E,点F与点E关于点B对称.
(1)求证:∠CFE=∠AFE;
(2)在y轴上是否存在这样的点P,使△AFP与△FBC相似,若有,请求出所有符合条件的点P的坐标;若没有,请说明理由.
(1)见解析(2)是P (0,-2),P
(0,-2),P (0,-
(0,- )
)
解析试题分析: (1)过点A作AM∥x轴,交FC于点M,交BE于点N.
∴AN=4.
设直线AC的解析式为 ,
,
则有 ,解得
,解得 .
.
∴直线AC的解析式为 当x=4时,
当x=4时,
∴点E的坐标为(4,4),
∵点F与E关于点D对称,则点F的坐标为(4,-8)
设直线FC的解析式为 ,
,
则有 ,解得
,解得 .
.
∴直线FC的解析式为
∵AM与x轴平行,则点M的纵坐标为6.
当y=6时,则有 解得x=8.
解得x=8.
∴AM="8," MN=AM—MN=4,
∴AN=MN,
∵FN⊥AM,
∴∠ANF=∠MNF,
又NF=NF,
∴△ANF≌△MNF,
∴∠CFE=∠AFE.
(2)∵C的坐标为(7, ),F坐标为(4,-8)
),F坐标为(4,-8)
∴
∵又A的坐标为(0,6),则 ,
,
又BF=6,
∵EF∥AO,则有∠PAF=∠AFE,
又由(2)可知∠BFC=∠AFE,
∴∠PAF=∠BFC.
①△AFP ∽△FCB,
∽△FCB,
则 ,即
,即 ,解得P
,解得P A="8."
A="8."
∴OP =8-6=2,
=8-6=2,
∴P 的坐标为(0,-2).
的坐标为(0,-2).
②若△AFP ∽△FBC,
∽△FBC,
则 ,即
,即 ,解得P
,解得P A=
A= .
.
∴OP =
= -6=
-6= ,
,
∴P 的坐标为(0,-
的坐标为(0,- ).
).
所以符合条件的点P的坐标有两个,分别是P (0,-2),P
(0,-2),P (0,-
(0,- ).
).
考点:本题考查了三角形全等
点评:此类试题属于难度很大的综合性试题,考生在解答此类试题时要注意掌握好一些基本知识

练习册系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )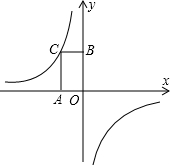 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=