题目内容
在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.
(1)求证:AC⊥ED
(2)求证:△ACD≌△ACE
(3)请猜测CD与DH的数量关系,并证明
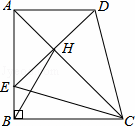
证(1)
:∵∠BAD=90°,AB=BC,
∴∠BAC=45°,
∴∠CAD=∠BAD﹣∠BAC=90°﹣45°=45°,
∴∠BAC=∠CAD,
∴AH⊥ED,
即AC⊥ED---------------2分
(2)
∵∠BAD=90°,AB=BC,
∴∠BAC=45°,
∴∠CAD=∠BAD﹣∠BAC=90°﹣45°=45°,
∴∠BAC=∠CAD,--------------3分
在△ACD和△ACE中,
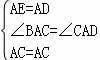 ,
,
∴△ACD≌△ACE(SAS),-------------5分
(3) CD=2DH------------6分
∵ △ACD≌△ACE
∴CD=CE,
∵∠BCE=15°,
∴∠BEC=90°﹣∠BCE=90°﹣15°=75°,
∴∠CED=180°﹣∠BEC﹣∠AED=180°﹣75°﹣45°=60°,
∴△CDE为等边三角形,
∴∠DCH=30°,-------------8分
∴CD=2DH,-------------10分

练习册系列答案
相关题目
 必有实数根
必有实数根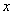 <0时,
<0时,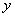 随
随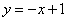 (B)
(B)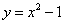 (C)
(C) (D)
(D)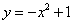
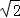 ,点E在对角线BD上,且
,点E在对角线BD上,且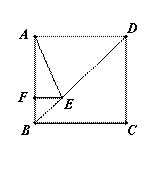 ∠BAE=
∠BAE=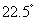 ,EF⊥AB,垂足为点F,
,EF⊥AB,垂足为点F,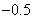
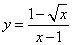 有意义的x的取值范围是 ;
有意义的x的取值范围是 ;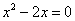 的解为
的解为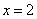 B.
B. 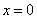 C.
C.  或
或 D.
D.