题目内容
如图,已知抛物线 与坐标轴交于
与坐标轴交于 三点,点
三点,点 的横坐标为
的横坐标为 ,过点
,过点 的直线
的直线 与
与 轴交于点
轴交于点 ,点
,点 是线段
是线段 上的一个动点,
上的一个动点, 于点
于点 .若
.若 ,且
,且 .
.

(1)求 的值
的值
(2)求出点 的坐标(其中
的坐标(其中 用含
用含 的式子表示):
的式子表示):
(3)依点 的变化,是否存在
的变化,是否存在 的值,使
的值,使 为等腰三角形?
为等腰三角形?
(1)b= ,c=3;
,c=3;
(2)B(4,0),P(4﹣4t,3t),Q(4t,0);
(3)当t= 或
或 或
或 时,△PQB为等腰三角形.
时,△PQB为等腰三角形.
【解析】
试题分析:(1)将A、C的坐标代入抛物线中即可求得待定系数的值.
(2)根据抛物线的解析式可求得B点的坐标,即可求出OB,BC的长,在直角三角形BPH中,可根据BP的长和∠CBO三角函数求出PH,BH的长,进而可求出OH的长,也就求出了P点的坐标.Q点的坐标,可直接由直线CQ的解析式求得.
(3)本题要分情况讨论:
①PQ=PB,此时BH=QH= BQ,在(2)中已经求得了BH的长,BQ的长可根据B、Q点的坐标求得,据此可求出t的值.
BQ,在(2)中已经求得了BH的长,BQ的长可根据B、Q点的坐标求得,据此可求出t的值.
②PB=BQ,那么BQ=BP=5t,由此可求出t的值.
③PQ=BQ,已经求得了BH的长,可表示出QH的长,然后在直角三角形PQH中,用BQ的表达式表示出PQ,即可用勾股定理求出t的值.
试题解析:(1)已知抛物线过A(﹣1,0)、C(0,3),则有:
 ,
,
解得 ,
,
因此b= ,c=3;
,c=3;
(2)令抛物线的解析式中y=0,则有﹣ x2+
x2+ x+3=0,
x+3=0,
解得x=﹣1,x=4;
∴B(4,0),OB=4,
因此BC=5,
在直角三角形OBC中,OB=4,OC=3,BC=5,
∴sin∠CBO= ,cos∠CBO=
,cos∠CBO= ,
,
在直角三角形BHP中,BP=5t,
因此PH=3t,BH=4t;
∴OH=OB﹣BH=4﹣4t,
因此P(4﹣4t,3t).
令直线的解析式中y=0,则有0=﹣ x+3,x=4t,
x+3,x=4t,
∴Q(4t,0);
(3)存在t的值,有以下三种情况
①如图1,当PQ=PB时,
∵PH⊥OB,则QH=HB,
∴4﹣4t﹣4t=4t,
∴t= ,
,
②当PB=QB得4﹣4t=5t,
∴t= ,
,
③当PQ=QB时,在Rt△PHQ中有QH2+PH2=PQ2,
∴(8t﹣4)2+(3t)2=(4﹣4t)2,
∴57t2﹣32t=0,
∴t= ,t=0(舍去),
,t=0(舍去),
又∵0<t<1,
∴当t= 或
或 或
或 时,△PQB为等腰三角形.
时,△PQB为等腰三角形.
考点:二次函数综合题.

 53随堂测系列答案
53随堂测系列答案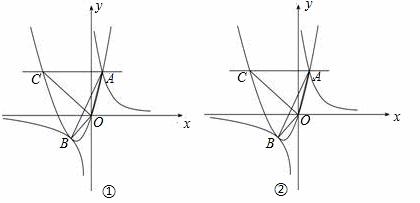
 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B. 上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐