题目内容
若一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2.
(1)利用配方法求出求根公式;
(2)用求根公式求证: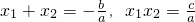 ;
;
(3)设方程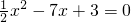 有两个实数根x1,x2,利用(2)的结论,不解方程求:①x12+x22;②
有两个实数根x1,x2,利用(2)的结论,不解方程求:①x12+x22;②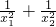 .
.
解:(1)ax2+bx+c=0(a≠0)
∵a≠0,∴两边同时除以a得:
二次项系数化为“1”得:x2+ x+
x+ =0
=0
移项得:x2+ x=-
x=-
配方得:x2+2•x• +
+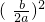 =
=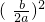 -
-
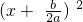 =
=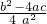
∵a≠0,∴4a2>0
当b2-4ac≥0时,直接开平方得:
x+ =
=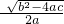
∴x=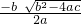 ,
,
∴x1=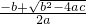 ,x2=
,x2=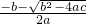 ;
;
(2)对于方程:ax2+bx+c=0(a≠0,且a,b,c是常数),
当△≥0时,利用求根公式,得
x1=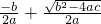 ,x2=
,x2=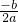 -
-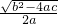 .
.
∵x1+x2=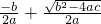 +
+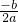 -
-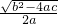 =-
=- ,
,
x1x2=(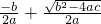 )•(
)•( 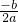 -
-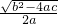 )=(
)=( 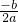 )2-(
)2-( 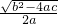 )2=
)2= .
.
∴x1+x2=- ,x1x2=
,x1x2= 是正确的;
是正确的;
(3)方程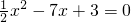 中,
中,
∵a= ,b=-7,c=3,
,b=-7,c=3,
∴b2-4ac=49-6=43>0,
则x1+x2=- =-
=-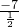 =14,x1x2=
=14,x1x2= =
=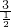 =6,
=6,
①x12+x22=(x1+x2)2-2x1x2=142-2×6=196-12=184;
②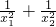 =
=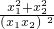 =
=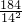 =
=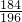 =
=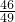 .
.
分析:(1)由a不为0,在方程两边同时除以a,把二次项系数化为1,然后把常数项移项到方程右边,两边都加上一次项系数一半的平方即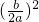 ,左边变为完全平方式,右边大于等于0时,开方即可得到求根公式;
,左边变为完全平方式,右边大于等于0时,开方即可得到求根公式;
(2)由求根公式求出的两个根相加、相乘,化简后即可得证;
(3)找出原方程的a,b及c的值,计算出b2-4ac,其值大于0,故方程有两个不等的实数根,根据(2)的结论求出两根之和与两根之积,
①把原式配方后变为关于两个根相加及相乘的形式,把求出的两个之和与两根之积代入即可求出值;
②把原式通分后分子利用①求出的结果整体代入,分母变为两根之积的平方,将两根之积代入,即可求出值.
点评:此题考查了利用配方法推导求根公式,由求根公式推导根与系数的关系,以及根与系数关系的运用,其中利用配方法推导求根公式是一个难点,要求学生必须掌握推导过程每一步的依据,即要搞清为什么,根与系数关系应用的前提必须是一元二次方程有解,即b2-4ac≥0,在运用根与系数关系时,往往利用配方,提取公因式,通分等方法把所求的式子化为与两根之和及两根之积有关的式子,然后把求出的两根之和与两根之积整体代入即可求出值.
∵a≠0,∴两边同时除以a得:
二次项系数化为“1”得:x2+
 x+
x+ =0
=0移项得:x2+
 x=-
x=-
配方得:x2+2•x•
 +
+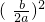 =
=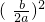 -
-
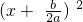 =
=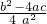
∵a≠0,∴4a2>0
当b2-4ac≥0时,直接开平方得:
x+
 =
=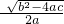
∴x=
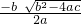 ,
,∴x1=
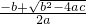 ,x2=
,x2=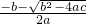 ;
;(2)对于方程:ax2+bx+c=0(a≠0,且a,b,c是常数),
当△≥0时,利用求根公式,得
x1=
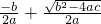 ,x2=
,x2=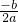 -
-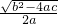 .
.∵x1+x2=
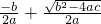 +
+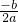 -
-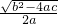 =-
=- ,
,x1x2=(
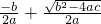 )•(
)•( 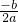 -
-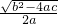 )=(
)=( 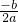 )2-(
)2-( 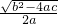 )2=
)2= .
.∴x1+x2=-
 ,x1x2=
,x1x2= 是正确的;
是正确的;(3)方程
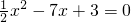 中,
中,∵a=
 ,b=-7,c=3,
,b=-7,c=3,∴b2-4ac=49-6=43>0,
则x1+x2=-
 =-
=-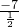 =14,x1x2=
=14,x1x2= =
=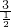 =6,
=6,①x12+x22=(x1+x2)2-2x1x2=142-2×6=196-12=184;
②
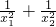 =
=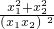 =
=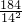 =
=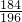 =
=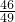 .
.分析:(1)由a不为0,在方程两边同时除以a,把二次项系数化为1,然后把常数项移项到方程右边,两边都加上一次项系数一半的平方即
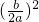 ,左边变为完全平方式,右边大于等于0时,开方即可得到求根公式;
,左边变为完全平方式,右边大于等于0时,开方即可得到求根公式;(2)由求根公式求出的两个根相加、相乘,化简后即可得证;
(3)找出原方程的a,b及c的值,计算出b2-4ac,其值大于0,故方程有两个不等的实数根,根据(2)的结论求出两根之和与两根之积,
①把原式配方后变为关于两个根相加及相乘的形式,把求出的两个之和与两根之积代入即可求出值;
②把原式通分后分子利用①求出的结果整体代入,分母变为两根之积的平方,将两根之积代入,即可求出值.
点评:此题考查了利用配方法推导求根公式,由求根公式推导根与系数的关系,以及根与系数关系的运用,其中利用配方法推导求根公式是一个难点,要求学生必须掌握推导过程每一步的依据,即要搞清为什么,根与系数关系应用的前提必须是一元二次方程有解,即b2-4ac≥0,在运用根与系数关系时,往往利用配方,提取公因式,通分等方法把所求的式子化为与两根之和及两根之积有关的式子,然后把求出的两根之和与两根之积整体代入即可求出值.

练习册系列答案
相关题目
 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的最大值.
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的最大值.