Question

如图，△ABC中，已知∠BAC＝45°，AD⊥BC于D，BD＝2，DC＝3，求AD的长。小萍同学灵活运用轴对称知识，将图形进行翻折变换，巧妙地解答了此题.请按照小萍的思路，探究并解答下列问题：

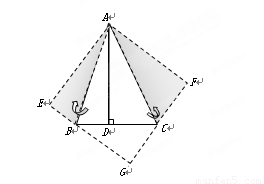
（1）AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D点的对称点为E、F，延长EB、FC相交于G点，证明四边形AEGF是正方形；

（2)设AD=x，利用勾股定理，建立关于x的方程模型，求出x的值.

 

Answer 1

【答案】

（1）四边形AEGF是正方形; （2）x=12．

【解析】

试题分析：（1）先根据△ABD≌△ABE，△ACD≌△ACF，得出∠EAF=90°；再根据对称的性质得到AE=AF，从而说明四边形AEGF是正方形；

（2）利用勾股定理，建立关于x的方程模型（x﹣4）²+（x﹣6）²=10²，求出AD=x=12．

试题解析：（1）证明：由题意可得：△ABD≌△ABE，△ACD≌△ACF．

∴∠DAB=∠EAB，∠DAC=∠FAC，又∠BAC=45°，

∴∠EAF=90°．

又∵AD⊥BC

∴∠E=∠ADB=90°，∠F=∠ADC=90°．

∴四边形AEGF是矩形，

又∵AE=AD，AF=AD

∴AE=AF．

∴矩形AEGF是正方形．

（2）解：设AD=x，则AE=EG=GF=x．

∵BD=4，DC=6

∴BE=4，CF=6

∴BG=x﹣4，CG=x﹣6

在Rt△BGC中，BG²+CG²=BC²，

∴（x﹣4）²+（x﹣6）²=10²．

化简得，x²﹣10x﹣24=0

解得x₁=12，x₂=﹣2（舍去）

所以AD=x=12．

考点:折叠问题；全等三角形的判定与性质；勾股定理.