题目内容
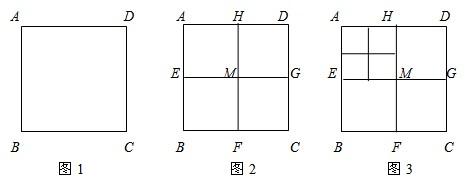
将正方形ABCD(如图1)作如下划分:
第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;
第2次划分:将图2左上角正方形AEMH按上述方法再作划分,得图3,则图3中共有________个正方形;
若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有________个正方形;
继续划分下去,能否将正方形ABCD划分成有2011个正方形的图形?需说明理由.

9. 401.
分析:本题需先根据图形,得出第2次划分共有多少个正方形,找出规律,得出n个的时候有多少个,从而得出结果.
解答:∵第一次划分,得出5个正方形,
∴第2次划分,根据图形得出共有9个正方形;
∴依题意得:第n次划分后,图中共有4n+1个正方形
∴第100次划分后,共有401个正方形;
∵第n次划分后,图中共有4n+1个正方形,
∴方程4n+1=2011没有整数解,
∴不能得到2011个正方形.
点评:本题主要考查了图形的变化类问题,在解题时要根据已知条件,找出规律是解题的关键.
分析:本题需先根据图形,得出第2次划分共有多少个正方形,找出规律,得出n个的时候有多少个,从而得出结果.
解答:∵第一次划分,得出5个正方形,
∴第2次划分,根据图形得出共有9个正方形;
∴依题意得:第n次划分后,图中共有4n+1个正方形
∴第100次划分后,共有401个正方形;
∵第n次划分后,图中共有4n+1个正方形,
∴方程4n+1=2011没有整数解,
∴不能得到2011个正方形.
点评:本题主要考查了图形的变化类问题,在解题时要根据已知条件,找出规律是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
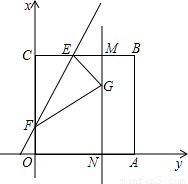
 (3,0),MN平行于y轴,E是BC的中点,现将纸片折叠,使点C落在MN上,折痕为直线EF,
(3,0),MN平行于y轴,E是BC的中点,现将纸片折叠,使点C落在MN上,折痕为直线EF,

 (3,0),MN平行于y轴,E是BC的中点,现将纸片折叠,使点C落在MN上,折痕为直线EF,
(3,0),MN平行于y轴,E是BC的中点,现将纸片折叠,使点C落在MN上,折痕为直线EF,