题目内容
 如图,边长为
如图,边长为 的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为
的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为
- A.

- B.3-

- C.

- D.3-

B
分析:连接AE,根据∠BAB′=30°可知∠DAB′=60°,由正方形的性质可知,AB=AD,由图形旋转的性质可知AD=AB′,故可得出Rt△ADE≌Rt△AB′E,由直角三角形的性质可得出DE的长,再由S阴影=S正方形ABCD-S四边形ADEB′即可得出结论.
解答: 解:连接AE,
解:连接AE,
∵∠BAB′=30°,
∴∠DAB′=60°,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠B=90°,
∵正方形AB′C′D′是正方形ABCD旋转而成,
∴AD=AB′,∠B′=90°,
在Rt△ADE与Rt△AB′E中,AD=AB′,AE=AE,
∴Rt△ADE≌Rt△AB′E,
∴∠DAE= =30°,
=30°,
∴DE=AD•tan∠DAE= ×
× =1,
=1,
∴S四边形ADEB′=2S△ADE=2× ×AD×DE=
×AD×DE= ,
,
∴S阴影=S正方形ABCD-S四边形ADEB=3- .
.
故选B.
点评:本题考查的是图形旋转的性质,涉及到正方形的性质、锐角三角函数的定义及特殊角的三角函数值,涉及面较广,难度适中.
分析:连接AE,根据∠BAB′=30°可知∠DAB′=60°,由正方形的性质可知,AB=AD,由图形旋转的性质可知AD=AB′,故可得出Rt△ADE≌Rt△AB′E,由直角三角形的性质可得出DE的长,再由S阴影=S正方形ABCD-S四边形ADEB′即可得出结论.
解答:
 解:连接AE,
解:连接AE,∵∠BAB′=30°,
∴∠DAB′=60°,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠B=90°,
∵正方形AB′C′D′是正方形ABCD旋转而成,
∴AD=AB′,∠B′=90°,
在Rt△ADE与Rt△AB′E中,AD=AB′,AE=AE,
∴Rt△ADE≌Rt△AB′E,
∴∠DAE=
 =30°,
=30°,∴DE=AD•tan∠DAE=
 ×
× =1,
=1,∴S四边形ADEB′=2S△ADE=2×
 ×AD×DE=
×AD×DE= ,
,∴S阴影=S正方形ABCD-S四边形ADEB=3-
 .
.故选B.
点评:本题考查的是图形旋转的性质,涉及到正方形的性质、锐角三角函数的定义及特殊角的三角函数值,涉及面较广,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
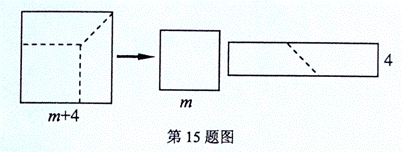



 的正方形纸片剪出一个边长为
的正方形纸片剪出一个边长为 的正方形之后,剩余部分又剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是( )
的正方形之后,剩余部分又剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是( )




 的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形,若拼成的矩形一边长为4,则另一边长为
的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形,若拼成的矩形一边长为4,则另一边长为

 的正方形纸片剪出一个边长为
的正方形纸片剪出一个边长为 的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是
的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是

 C.
C. D.
D.