Question

在正方形ABCD中，AC为对角线，E为AC上一点，连接EB、ED

1.求证：△BEC≌△DEC；

2.延长BE交AD于F，当∠BED＝120°时，求的度数．

 

Answer 1

 

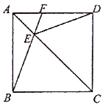
1.∵四边形ABCD是正方形，

∴BC＝DC

又∵AC为对角线，E为AC上一点，

∴∠BCE＝∠DCE＝45°．

∵EC＝EC,

∴△BEC≌△DEC(SAS)；…………………………………………3分

2.∵△BEC≌△DEC, ∠BED＝120°,

∴∠BEC＝∠DEC＝60°．

∵∠DAC＝45°，

∴∠ADE＝15°

∴∠EFD＝∠BED－∠ADE＝120°－15°＝105°………………………7分

解析:（1）在证明△BEC≌△DEC时，根据题意知，运用SAS定理就行；

（2）根据全等三角形的性质知对应角相等，即∠BEC=∠DEC=∠BED，又由对顶角相等、三角形的一个内角的补角是另外两个内角的和求得∠EFD=∠BEC+∠CAD．