题目内容
已知关于x的两个一元二次方程:
方程①:  ; 方程②:
; 方程②:  .
.
(1)若方程①有两个相等的实数根,求解方程②;
(2)若方程①和②中只有一个方程有实数根, 请说明此时哪个方程没有实数根, 并化
简 ;
;
(3)若方程①和②有一个公共根a, 求代数式 的值.
的值.
(1)∵方程①有两个相等实数根,
|
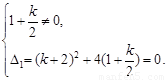
由③得k + 2 ¹0,
由④得 (k + 2) (k+4) =0.
∵ k + 2¹0,
∴ k=-4. …………………………1分
当k=-4时, 方程②为: 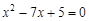 .
.
解得  …………………………2分
…………………………2分
(2)由方程②得 2= 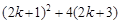 .
.
法一2-1=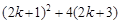 -(k
+ 2) (k+4) =3k2+6k+5
=3(k+1)2+2>0.
-(k
+ 2) (k+4) =3k2+6k+5
=3(k+1)2+2>0.
∴ 2>1. …………………………………………………3分
∵ 方程①、②只有一个有实数根,
∴ 2>0> 1.
∴ 此时方程①没有实数根. ………………………………4分
由

得 (k + 2) (k+4)<0. ………………………………5分
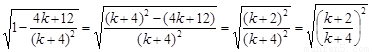 .
.
∵ (k + 2) (k+4)<0,
∴
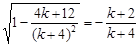 .
………………………………6分
.
………………………………6分
法二: ∵
2=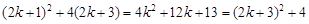 >0.
>0.
因此无论k为何值时, 方程②总有实数根. …………………………………3分
∵ 方程①、②只有一个方程有实数根,
∴ 此时方程①没有实数根. …………………………………4分
下同解法一.
( 3) 法一: ∵ a 是方程①和②的公共根,
∴ 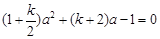 ;
;
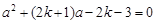 .
.
|
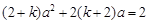 ,
,  .
.
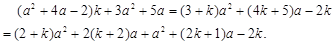
=2+3=5. ……………………………………………8分
法二: ∵ a 是方程①和②的公共根,
∴ 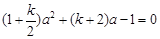 ;
③
;
③ 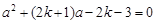 . ④
. ④
∴(③-④)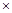 2得
2得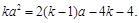 ⑤
⑤
由④得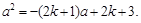 ⑥
…………………………7分
⑥
…………………………7分
将⑤、⑥代入原式,得
原式=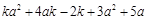
=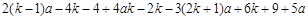
=5. ……………………………………………8分
【解析】略

 ; 方程②:
; 方程②:  .
. ; 方程②:
; 方程②:  .
. ;
; 的值.
的值.