Question

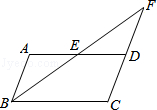
如图，在▱ABCD中，E为CD上一点，连接AE、BD，且AE、BD交于点F，S_△DEF：S_△ABF=4：25，则DE：EC=（　　）

A．

2：5

B．

2：3

C．

3：5

D．

3：2

Answer 1

考点：

相似三角形的判定与性质；平行四边形的性质．

分析：

先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF，再根据S_△DEF：S_△ABF=4：10：25即可得出其相似比，由相似三角形的性质即可求出 DE：EC的值，由AB=CD即可得出结论．

解答：

解：∵四边形ABCD是平行四边形，

∴AB∥CD，

∴∠EAB=∠DEF，∠AFB=∠DFE，

∴△DEF∽△BAF，

∵S_△DEF：S_△ABF=4：25，

∴DE：AB=2：5，

∵AB=CD，

∴DE：EC=2：3．

故选B．

点评：

本题考查的是相似三角形的判定与性质及平行四边形的性质，熟知相似三角形边长的比等于相似比，面积的比等于相似比的平方是解答此题的关键．