Question

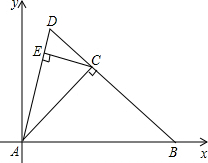已知△ABD中，∠ABD=45°，∠DAB=75°，AC⊥BD于点C，CE⊥AD于点E，且C（2

3

，2

3

），求点E的坐标．

Answer 1

考点：勾股定理,坐标与图形性质,解直角三角形

专题：

分析：作CF⊥AB，据C点坐标即可求得AC的长度，根据∠BAD即可求得AE的长度，计算tan∠BAD即可求得直线AD解析式，即可解题．

解答：解：作CF⊥AB，

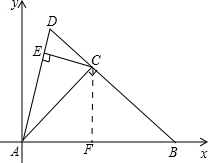
∴AF=CF=2

3

，
∴AC=2

6

，
∵∠BAD=75°，∠BAC=45°，
∴∠DAC=30°，
∴AE=AC•cos∠CAE=3

2

，
∵tan∠BAD=tan（30°+45°）=

tan45°+tan30°

1-tan45°•tan30°

=2+

3

，
∴直线AD解析式为y=（2+

3

）x，
设E点坐标[x，（2+

3

）x]，
则x²+(2x+

3

x)2=AE²，
解得：x=

3

3 +1

=

3 3 -3

2

，
∴（2+

3

）x=

3

3 +1

×（2+

3

）=

3+3 3

2

，
∴E点坐标为（

3 3 -3

2

，

3+3 3

2

）．

点评：本题考查了特殊角的三角函数值，考查了角的和的正切值的计算，考查了直角三角形中三角函数的运用，本题中求直线AD解析式是解题的关键．