题目内容
一元二次方程x2-5x+1=0的两根为x1、x2，则数组（x1+x2，x12+x22）是
- A.（-5，23）
- B.（5，23）
- C.（-5，21）
- D.（5，21）
B
分析：由根与系数的关系可得：x1+x2=5，x1•x2=1，而x12+x22=（x1+x2）2-2x1•x2，所以可以利用前面的结论求出其结果，最后判断哪个正确．
解答：由根与系数的关系可得：
x1+x2=5，
x1•x2=1，
x12+x22=（x1+x2）2-2x1•x2=52-2=23，
∴数组（x1+x2，x12+x22）是（5，23）．
故选B．
点评：本题考查一元二次方程根与系数的关系．
分析：由根与系数的关系可得：x1+x2=5，x1•x2=1，而x12+x22=（x1+x2）2-2x1•x2，所以可以利用前面的结论求出其结果，最后判断哪个正确．
解答：由根与系数的关系可得：
x1+x2=5，
x1•x2=1，
x12+x22=（x1+x2）2-2x1•x2=52-2=23，
∴数组（x1+x2，x12+x22）是（5，23）．
故选B．
点评：本题考查一元二次方程根与系数的关系．
练习册系列答案
相关题目
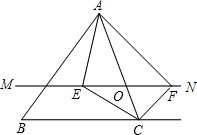从甲、乙两题中选做一题，如果两题都做，只以甲题计分．