题目内容
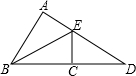如图△BAE≌△BCE；△BAE≌△DCE，则∠D=________．
30°
分析：根据题意，三个三角形全等，所以∠A=∠BCE=∠DCE，∠D=∠ABE=∠CBE，根据∠BCE+∠DCE=180°，所以∠A=∠BCE=∠DCE=90°，根据三角形内角和定理3∠D+90°=180°，求解即可．
解答：∵△BAE≌△BCE，△BAE≌△DCE，
∴△BAE≌△BCE≌△DCE，
∴∠A=∠BCE=∠DCE，∠D=∠ABE=∠CBE，
∴∠ABD=2∠D，
∵∠BCE+∠DCE=180°，
∴∠A=∠BCE=∠DCE=90°，
在△ABD中，∠D+2∠D+90°=180°，
解得∠D=30°．
点评：本题主要考查全等三角形对应角相等的性质，根据相等的两角的和等于180°，求出每一个角等于90°，即∠A等于90°是求解本题的关键．
分析：根据题意，三个三角形全等，所以∠A=∠BCE=∠DCE，∠D=∠ABE=∠CBE，根据∠BCE+∠DCE=180°，所以∠A=∠BCE=∠DCE=90°，根据三角形内角和定理3∠D+90°=180°，求解即可．
解答：∵△BAE≌△BCE，△BAE≌△DCE，
∴△BAE≌△BCE≌△DCE，
∴∠A=∠BCE=∠DCE，∠D=∠ABE=∠CBE，
∴∠ABD=2∠D，
∵∠BCE+∠DCE=180°，
∴∠A=∠BCE=∠DCE=90°，
在△ABD中，∠D+2∠D+90°=180°，
解得∠D=30°．
点评：本题主要考查全等三角形对应角相等的性质，根据相等的两角的和等于180°，求出每一个角等于90°，即∠A等于90°是求解本题的关键．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
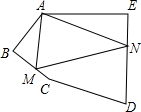如图，五边形ABCDE中，∠BAE=120°，∠B=∠E=90°，AB=BC=1，AE=DE=2，在BC、DE上分别找一点M、N，使△AMN的周长最小，则△AMN的周长最小值为（ ）
