题目内容
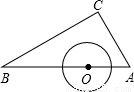
如图，在三角板ABC中，∠C=90°，∠B=30°，O为AB上一点，⊙O的半径为1，现将三角板平移，使AC与⊙O相切，则AO=分析：设AC与⊙O相切于点D，连接OD，则在直角△OAD中，已知∠A与OD的长，利用正弦函数即可求得OA的长．
解答：
解：设AC与⊙O相切于点D，连接OD．
在直角△ABC中，∠B=90°-∠A=90°-30°=60°．
∵AC是⊙O的切线，
∴OD⊥AC，且OD=1．
∴在直角△OAD中，sinA=
，
∴OA=
=
=
=
．
故答案是：
．
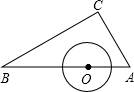
解：设AC与⊙O相切于点D，连接OD．在直角△ABC中，∠B=90°-∠A=90°-30°=60°．
∵AC是⊙O的切线，
∴OD⊥AC，且OD=1．
∴在直角△OAD中，sinA=
| OD |
| OA |
∴OA=
| OD |
| sinA |
| 1 |
| sin60° |
| 1 | ||||
|
2
| ||
| 3 |
故答案是：
2
| ||
| 3 |
点评：本题考查了切线的性质以及三角函数．已知圆的切线，常用的辅助线是连接圆心与切点，利用垂直关系．
练习册系列答案
名师点拨卷系列答案
相关题目
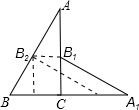如图，直角三角板ABC中，∠A=30°，BC=3cm，将直角三角板绕顶点C按顺时针方向旋转90°至△A1B1C的位置，沿CB向左平移使B1点落在△ABC的斜边AB上，点B1平移到点B2，则点B由B?B1?B2运动的路程是（ ）A、（3π+3-
| ||||
B、（3π-3+
| ||||
C、（
| ||||
D、（
|
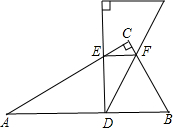使这个30°角的两边分别与△ABC的边AC，BC相交于点E，F，且使DE始终与AB垂直．
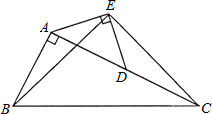如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点．将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A、D重合，连接BE、EC．