题目内容
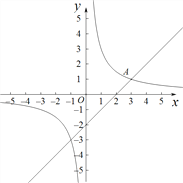
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象与直线y=x-2交于点A(a,1).
的图象与直线y=x-2交于点A(a,1).
(1)求a,k的值;
(2)已知点P(m,0)(1≤m< 4),过点P作平行于y轴的直线,交直线y=x-2于点M (x1,y1),交函数![]() 的图象于点N(x1,y2),结合函数的图象,直接写出
的图象于点N(x1,y2),结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)3;(2)![]() .
.
【解析】
(1)将点A(a,1)代入y=x-2可求得a的值,并由此可得点A的坐标,将所得点A的坐标代入反比例函数![]() 的解析式即可求得k的值;
的解析式即可求得k的值;
(2)根据题意和已知条件画出符合要求的图形,结合图形即可得到所求取值范围.
(1)∵直线y=x-2经过点A(a,1),
∴a=3.
∴A(3,1).
∵函数![]() 的图象经过点A(3,1),
的图象经过点A(3,1),
∴k=3.
(2)如图1可知:![]() 的取值范围是
的取值范围是![]() .
.


 高中必刷题系列答案
高中必刷题系列答案【题目】市园林处为了对一段公路进行绿化,计划购买![]() ,
,![]() 两种风景树共900棵.
两种风景树共900棵.![]() ,
,![]() 两种树的相关信息如下表:
两种树的相关信息如下表:
品种 项目 | 单价(元 | 成活率 |
| 80 |
|
| 100 |
|
若购买![]() 种树
种树![]() 棵,购树所需的总费用为
棵,购树所需的总费用为![]() 元.
元.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若购树的总费用不超过82 000元,则购![]() 种树不少于多少棵?
种树不少于多少棵?
(3)若希望这批树的成活率不低于![]() ,且使购树的总费用最低,应选购
,且使购树的总费用最低,应选购![]() ,
,![]() 两种树各多少棵?此时最低费用为多少?
两种树各多少棵?此时最低费用为多少?
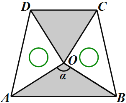
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.

(1)请补全下表:
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
(2)填空:
由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,![]() ;当α=135°时,
;当α=135°时,![]() .由上表可以得到
.由上表可以得到![]() ( ______°);
( ______°);![]() ( ______°),…,由此可以归纳出
( ______°),…,由此可以归纳出![]() .
.
(3) 两块相同的等腰直角三角板按如图的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
【题目】某超市电器销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售量 | 销售收入 | |
A型号 | B型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能请给出采购方案.若不能,请说明理由.