题目内容

如图，给出下列四个条件，不能判断△ABC≌△A′B′C′的是
①∠B=∠B′②∠C=∠C′
③AC=A′C′④BC=B′C′．


  1. A.
    ①②③
  2. B.
    ①②④
  3. C.
    ①③④
  4. D.
    ②③④
C
分析：由题意，结合全等三角形的判定定理：“AAS”，“ASA”，“SAS”，即可推出A，B，D三项都可推出两三角形全等，只有C项不可以推出两三角形全等．
解答：A项，根据全等三角形的判定定理“AAS”，可推出两三角形全等，故本选项错误；
B项，根据全等三角形的判定定理“ASA”，可推出两三角形全等，故本选项错误；
C项，“SSA”不能推出两三角形全等，故本选项正确；
D项，根据全等三角形的判定定理“SAS”，可推出两三角形全等，故本选项错误．
故选择C．
点评：本题主要考查全等三角形的判定定理，关键在于熟练掌握各判定定理，认真分析每一选项中的条件的组合．
练习册系列答案
相关题目
18、探索下列问题：
（1）在图1给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分；
（2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2．①请你在图2中相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）；
②请你在图3中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）．
（3）是否存在一条直线，将一个任意的平面图形（如图4）分割成面积相等的两部分，请简略说出理由．
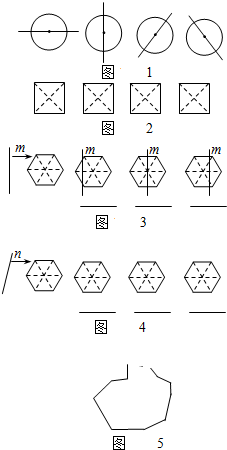（2013•池州一模）我们知道：由于圆是中心对称图形，所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分（如图1）．
探索下列问题：
（1）在如图2给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分；
（2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2．
①请你在如图3中相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）；
②请你在如图4中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）．
（3）是否存在一条直线，将一个任意的平面图形（如图5）分割成面积相等的两部分？请简略说出理由．
探索下列问题：
（1）在图1给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分；
（2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2．①请你在图2中相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）；
②请你在图3中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）．
（3）是否存在一条直线，将一个任意的平面图形（如图4）分割成面积相等的两部分，请简略说出理由．

精英家教网
探索下列问题：
（1）在图1给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分；
（2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2．①请你在图2中相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）；
②请你在图3中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）．
（3）是否存在一条直线，将一个任意的平面图形（如图4）分割成面积相等的两部分，请简略说出理由．
我们知道：由于圆是中心对称图形，所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分（如图1）．
探索下列问题：
（1）在如图2给出的四个正方形中，各画出一条直线（依次是：水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分；
（2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2．
①请你在如图3中相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）；
②请你在如图4中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式（用“＜”，“=”，“＞”连接）．
（3）是否存在一条直线，将一个任意的平面图形（如图5）分割成面积相等的两部分？请简略说出理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网