题目内容

6、如图，将直角三角形纸片（∠ACB=90°），沿线段MN折叠，使得A落在C处，若∠ACN=20°，则∠B的度数为（　　）
分析：根据折叠得到∠A=20°，再根据直角三角形的两个锐角互余即可求解．
解答：解：根据题意，得∠A=∠ACN=20°．
又∠ACB=90°，
∴∠B=90°-20°=70°．
故选B．
点评：此题综合运用了折叠的性质和直角三角形的两个锐角互余的性质．
练习册系列答案
相关题目
28、操作与探究：
（1）图①是一块直角三角形纸片．将该三角形纸片按如图方法折叠，是点A与点C重合，DE为折痕．试证明△CBE等腰三角形；
（2）再将图①中的△CBE沿对称轴EF折叠（如图②）．通过折叠，原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合（指无缝无重叠）所成的矩形，我们称这样的两个矩形为“组合矩形”．你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；
（3）请你在图④的方格纸中画出一个斜三角形，同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点（各小正方形的顶点）上；
（4）有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形（其中的内接矩形的四个顶点分别在原四边形的四条边上）．请你进一步探究，一个非特殊的四边形（指除平行四边形、梯形外的四边形）满足何条件时，一定能折成组合矩形？
△ABC是顶点在如图所示的方格纸中的格点上的三角形．
（1）在这个方格纸中，把△ABC向上平移5格，得△A1B1C1，再将△A1B1C1绕点C1按顺时针方向旋转180°得△A2B2C1，请在方格纸中画出△A1B1C1和△A2B2C1；
（2）若以点B为坐标原点，BC为x轴的正方向建立直角坐标系（方格纸中一个小正方形的边长为1个单位长），画出这个坐标系，写出第一次变换后所得△A1B1C1的各顶点和第二次变换后所得△A2B2C1的各顶点的坐标；并求A点经过2次变换后到达点A2所经过路径长度是多少个单位长？
直角三角形纸片ABC中，∠ACB=90°，AC≤BC，如图，将纸片沿某条直线折叠，使点A落在直角边BC上，记落点为D，设折痕与AB、AC边分别交于点E、点F．探究：如果折叠后的△CDF与△BDE均为等腰三角形，那么纸片中∠B的度数是多少？写出你的计算过程，并画出符合条件的折叠后的图形．
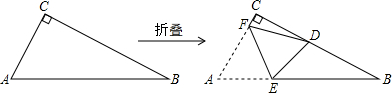
精英家教网

△ABC是顶点在如图所示的方格纸中的格点上的三角形．
（1）在这个方格纸中，把△ABC向上平移5格，得△A1B1C1，再将△A1B1C1绕点C1按顺时针方向旋转180°得△A2B2C1，请在方格纸中画出△A1B1C1和△A2B2C1；
（2）若以点B为坐标原点，BC为x轴的正方向建立直角坐标系（方格纸中一个小正方形的边长为1个单位长），画出这个坐标系，写出第一次变换后所得△A1B1C1的各顶点和第二次变换后所得△A2B2C1的各顶点的坐标；并求A点经过2次变换后到达点A2所经过路径长度是多少个单位长？
（2006•连云港）操作与探究：
（1）图①是一块直角三角形纸片．将该三角形纸片按如图方法折叠，是点A与点C重合，DE为折痕．试证明△CBE等腰三角形；
（2）再将图①中的△CBE沿对称轴EF折叠（如图②）．通过折叠，原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合（指无缝无重叠）所成的矩形，我们称这样的两个矩形为“组合矩形”．你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；
（3）请你在图④的方格纸中画出一个斜三角形，同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点（各小正方形的顶点）上；
（4）有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形（其中的内接矩形的四个顶点分别在原四边形的四条边上）．请你进一步探究，一个非特殊的四边形（指除平行四边形、梯形外的四边形）满足何条件时，一定能折成组合矩形？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网