题目内容
已知:如图所示,正方形ABCD和正方形AEFG有一个公共点A,连接BE、DG.
线段BE、DG有怎样的关系?请证明你的结论.

【答案】
见试题解析.
【解析】
试题分析:利用正方形的性质,找到三角形全等条件,证明三角形全等得到 ,延长
,延长 ,交
,交 与点
与点 ,连结
,连结 有以上三角形全等得
有以上三角形全等得 .
.
试题解析:
 四边
四边 形和四边形为
形和四边形为 正方形
正方形



 3分
3分
在△EAB和△GAD中,

∴△EAB≌△GAD(SAS) 5分
∴BE=DG 6分
延长BE,交DG与点H,连结BD
∵△EAB≌△GAD
∴∠EBA=∠GDA 7分
∵∠DAB=90°
∴∠ADB+∠DAB=90°
∴∠ADB+∠DAE+∠EBA=90° 8分
∴∠ADB+∠DAE+∠GDA=90°
∴∠DHB=90° ∴BE⊥DG 9分
考点:1.正方形的性质2.三角形全等判定和性质.

练习册系列答案
相关题目
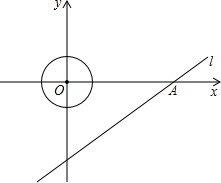 .5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间?
.5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间? 已知:如图所示,直线l的解析式为
已知:如图所示,直线l的解析式为 ,并且与x轴、y轴分别交于点A、B.
,并且与x轴、y轴分别交于点A、B.
 x-3,并且与x轴、y轴分别相交于点A、B.
x-3,并且与x轴、y轴分别相交于点A、B.
 x-3,并且与x轴、y轴分别相交于点A、B.
x-3,并且与x轴、y轴分别相交于点A、B.