题目内容
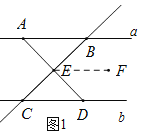
【题目】如图1，已知
，点
、
在直线
上，点
、
在直线
上，且
于
.
（1）求证：
；
（2）如图2，
平分
交
于点
，
平分
交
于点
，求
的度数；
（3）如图3，
为线段
上一点，
为线段上一点，连接
，
为
的角平分线上一点，且
，则
、
、
之间的数量关系是__________.
【答案】（1）见解析；（2）225°；（3）
或
【解析】
(1) 过
作EF∥a,由BC⊥AD可知
，由平行可知
，
，从而可得
=
+
=
(2)作
，
，设
，
，由平行线性质和邻补角定义可得
，
，进而计算出
即可解答，
（3）分两种情况解答：I.∠NCD在∠BCD内部，II
外部，仿照（2）解答即可.
（1）证明：过作
,
∴
∴
∴
∴
∴
（2）解：作，，
设，，
由（1）知：
，
，
，
∴
，
∴，
同理：，
∴
（3）结论：或，
I.∠NCD在∠BCD内部时，
过I点作
，过N点作
，设∠IPN=∠BPN=x，
=y，
∴∠BCD=3y.
∵a∥b，
∴
∴
，
，
，
∴
，
，
∴
，
∴
∴
II.
在
外部时,如图3（2）：
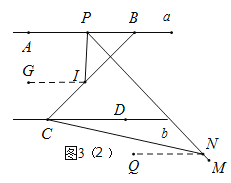
过I点作，过N点作，设∠IPN=∠BPN=x，=y，
∴∠BCD=y.
∵a∥b，
∴IG∥a∥
∴，，，
∴
，
，
∴，
∴
∴
练习册系列答案
相关题目
