题目内容
已知锐角△ABC中，∠A=60°，BD和CE都是△ABC的高．如果△ABC的面积为12，那么四边形BCDE的面积为________．
9
分析：根据∠A的度数和BD⊥AC，CE⊥AB，即可求得AB=2AD，AC=2AE，进而可以求得△ADE与△ABC的面积的比值，即可求得△ADE的面积，即可求得四边形BCED的面积，即可解题．
解答：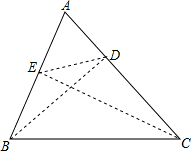
解：∵∠A=60°，BD⊥AC，CE⊥AB，
∴AB=2AD，AC=2AE，
∴△ADE的面积为
AD•AE•sinA，
△ABC的面积为AB•AC•sinA，
∴△ADE的面积为△ABC面积的
，
∴△ADE的面积为3，
∴四边形BCDE的面积为12-3=9．
故答案为：9．
点评：本题考查了三角形面积的计算，特殊角的三角函数值在直角三角形中的运用，本题中求得AB=2AD，AC=2AE是解题的关键．
分析：根据∠A的度数和BD⊥AC，CE⊥AB，即可求得AB=2AD，AC=2AE，进而可以求得△ADE与△ABC的面积的比值，即可求得△ADE的面积，即可求得四边形BCED的面积，即可解题．
解答：
解：∵∠A=60°，BD⊥AC，CE⊥AB，∴AB=2AD，AC=2AE，
∴△ADE的面积为
AD•AE•sinA，△ABC的面积为
AB•AC•sinA，∴△ADE的面积为△ABC面积的
，∴△ADE的面积为3，
∴四边形BCDE的面积为12-3=9．
故答案为：9．
点评：本题考查了三角形面积的计算，特殊角的三角函数值在直角三角形中的运用，本题中求得AB=2AD，AC=2AE是解题的关键．
练习册系列答案
相关题目
阅读材料，解答问题：
