题目内容
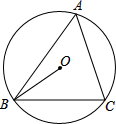如图，在⊙O中，已知∠OBC=40°，则∠BAC的度数为（ ）分析：首先连接OC，由等腰三角形的性质，可求得∠BOC的度数，又由圆周角定理，即可求得∠BAC的度数．
解答：
解：连接OC，
∵OB=OC，
∴∠OCB=∠OBC=40°，
∴∠BOC=180°-∠OBC-∠OCB=100°，
∴∠BAC=
∠BOC=50°．
故选B．
解：连接OC，∵OB=OC，
∴∠OCB=∠OBC=40°，
∴∠BOC=180°-∠OBC-∠OCB=100°，
∴∠BAC=
| 1 |
| 2 |
故选B．
点评：此题考查了圆周角定理以及等腰三角形的性质．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
22、如图，在△ABC中，已知B（-3，1）．
9、如图，在△ABC中，已知∠ABC和∠ACB的平分线相交于点D，过D点作EF∥BC，交AB于点E，交AC于点F，若BE+CF=9，则线段EF的长为（ ）
17、如图，在△ABC中，已知∠C=90°，BC=3，AC=4，则它的内切圆半径是
如图，在△ABC中，已知AB=AC=10，BC=16，O是△ABC的重心，则tan∠DBC的值是
如图，在△ABC中，已知AB=AC，D为AB上一点，且AD=CD=BC，则∠B=