Question

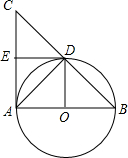（2012•广州模拟）如图，以△ABC的边AB为直径的⊙O交边BC于点D，其中边AC与⊙O相切于点A，E为AC中点．
（1）求证：∠CAD=∠B；
（2）求证：DE是⊙O切线．

Answer 1

分析：（1）利用直径所对的圆周角是直角的性质推知AD⊥BC；由切线的性质知AC⊥AB；所以∠CAD+∠DAB=∠DAB+∠B，即∠CAD=∠B；
（2）由于OD=OA，所以∠ODA=∠OAD，因为E为Rt△ACD的斜边AC的中点，所以CE=AD=DE，所以∠EDB=∠EBD，因为∠OAD+∠EAD=90°，所以∠ODA+∠EDA=90°，所以DE与半圆O相切．

解答：证明：（1）∵AC与⊙O相切于点A，
∴AC⊥AB，
∴∠CAB=90°；
又∵AB是⊙O的直径，
∴∠ADB=90°（直径所对的圆周角是直角），
∴∠CAD+∠DAB=∠DAB+∠B，即∠CAD=∠B；

（2）∵OD=OA，
∴∠ODA=∠OAD；
又∵E为Rt△ACD的斜边AC的中点，
∴CE=AE=DE，
∴∠EDA=∠EAD，
∵∠OAD+∠EAD=90°，
∴∠ODA+∠EDA=90°，
∴DE与半圆O相切．

点评：本题考查了切线的性质、圆周角定理．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．