题目内容
一次函数y=- x+1与x轴,y轴分别交于点A,B.以线段AB为边在第一象限内作正方形ABCD (如图).在第二象限内有一点P(a,
x+1与x轴,y轴分别交于点A,B.以线段AB为边在第一象限内作正方形ABCD (如图).在第二象限内有一点P(a, ),满足S△ABP=S正方形ABCD,则a= .
),满足S△ABP=S正方形ABCD,则a= .
【答案】分析:由已知条件易求得A,B两点的坐标,可求出正方形的边AB的长,这样正方形的面积可求得为4,于是问题转化为求a为多少时三角形ABP的面积为4的问题了,可作出辅助线利用面积差列出方程求解.
解答: 解:过点P作PE⊥x轴于点E,由已知得A(
解:过点P作PE⊥x轴于点E,由已知得A( ,0),B(0,1),
,0),B(0,1),
∴AB= =2,
=2,
∴S△ABP=S正方形ABCD=4,
又S△ABP=S梯形PEOB+S△OAB-S△APE,
∴ (
( +1)×|a|+
+1)×|a|+ ×1×
×1× -
- ×
× ×(|a|+
×(|a|+ )=4,
)=4,
解得a= -8.
-8.
故答案为: -8.
-8.
点评:本题考查了一次函数的综合应用及正方形的性质;利用面积差列出方程求解是正确解答本题的关键,一次函数题常常通过列方程来解答,这是一种非常重要的方法,应熟练掌握.
解答:
 解:过点P作PE⊥x轴于点E,由已知得A(
解:过点P作PE⊥x轴于点E,由已知得A( ,0),B(0,1),
,0),B(0,1),∴AB=
 =2,
=2,∴S△ABP=S正方形ABCD=4,
又S△ABP=S梯形PEOB+S△OAB-S△APE,
∴
 (
( +1)×|a|+
+1)×|a|+ ×1×
×1× -
- ×
× ×(|a|+
×(|a|+ )=4,
)=4,解得a=
 -8.
-8.故答案为:
 -8.
-8.点评:本题考查了一次函数的综合应用及正方形的性质;利用面积差列出方程求解是正确解答本题的关键,一次函数题常常通过列方程来解答,这是一种非常重要的方法,应熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为ycm,椅子的高度为xcm,则y应是x的一次函数,下表列出两套符合条件的课桌椅的高度:第一套第二套椅子高度xcm桌子高度ycm.
(1)请确定y与x的函数关系式.
(2)现有一把高39cm的椅子和一张高为78.2的课桌,它们是否配套?为什么?
| 第一套 | 第二套 | |
| 椅子高度xcm | 40 | 37 |
| 桌子高度ycm | 75 | 70 |
(2)现有一把高39cm的椅子和一张高为78.2的课桌,它们是否配套?为什么?
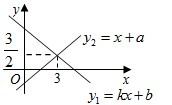 一次函数y1=kx+b与y2=x+a的图象如图,下列结论中:
一次函数y1=kx+b与y2=x+a的图象如图,下列结论中: