题目内容
 如图,已知△ABC是锐角三角形,分别以AB、AC为边向外侧作两个等边三角形△ABM和△CAN,D、E、F分别是MB,BC,CN的中点,连结DE、FE,求证:DE=EF.
如图,已知△ABC是锐角三角形,分别以AB、AC为边向外侧作两个等边三角形△ABM和△CAN,D、E、F分别是MB,BC,CN的中点,连结DE、FE,求证:DE=EF.
 证明:连接MC、BN,
证明:连接MC、BN,∵△ABM和△CAN是等边三角形,
∴∠BAM=∠CAN=60°,MA=BA,AN=AC
∴∠BAM+∠BAC=∠CAN+∠BAC,
即∠MAC=∠BAN,
在△MAC与△BAN中,
 ,
,∴△MAC≌△BAN(SAS),
∴MC=NB,
∵D、E、F分别是MB,BC,CN的中点,
∴DE=
 MC,EF=
MC,EF= BN,
BN,∴DE=EF.
分析:连接MC、BN,证明△MAC与△BAN全等,可得MC=BN.再通过三角形的中位线定理可证DE、EF分别是MC、BN的一半,从而可得DE=EF.
点评:此题主要考查了全等三角形的判定与性质,以及等边三角形的性质,三角形的中位线定理,关键是证明MC=BN.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的坐标为(-1,0).
的坐标为(-1,0). 如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.
如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.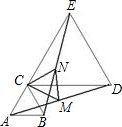 如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,
如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点, (2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF. (2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.
(2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.