题目内容
如图，已知：MN∥DQ，AC、BC分别平分∠BAN、∠ABQ，求证：AC⊥CB．
证明：∵MN∥DQ，∴∠NAB+∠QBA=180°．
∵AC、BC分别平分∠BAN、∠ABQ，
∴∠CAB=
∠NAB，∠CBA=∠QBA．
∴∠CAB+∠CBA=90°．
∴∠C=90°，即AC⊥BC．
分析：欲证AC⊥CB，即证∠C=90°．根据三角形内角和定理知需证明∠CAB+∠CBA=90°．运用平行线的性质和角平分线的定义证之．
点评：此题考查平行线的性质和垂线的定义，难度中等．
∵AC、BC分别平分∠BAN、∠ABQ，
∴∠CAB=
∠NAB，∠CBA=∠QBA．∴∠CAB+∠CBA=90°．
∴∠C=90°，即AC⊥BC．
分析：欲证AC⊥CB，即证∠C=90°．根据三角形内角和定理知需证明∠CAB+∠CBA=90°．运用平行线的性质和角平分线的定义证之．
点评：此题考查平行线的性质和垂线的定义，难度中等．
练习册系列答案
相关题目
13、如图，已知直线MN是△ABC中BC边上的垂直平分线，连接CM，若AB=12，AC=8，则△ACM的周长为
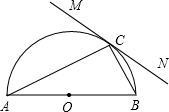如图，已知直线MN与以AB为直径的半圆相切于点C，∠A=28°．
16、如图，已知直线MN和MN外一点，请用尺规作图的方法完成下列作图：
如图，已知直线MN是线段AB的对称轴，CA交MN于D，若AC=6，BC=4，则△BCD的周长是