题目内容
如图，EF是正方形两对边中点的连线段，将∠A沿DK折叠，使它的顶点A落在EF上的G点，求∠DKG的度数．
解：∵DF=
CD=DG
∴∠DGF=30°．
∵∠EKG+∠KGE=90°
∠KGE+∠DGF=90°
∴∠EKG=∠DGF=30°．∵2∠DKG+∠GKE=180°
∴∠DKG=75°．
分析：利用DF=DG，可求出∠DGF，再求出∠GKE，利用2∠DKG+∠GKE=180°求出∠DKG的度数．
点评：考查了30°角所对的直角边等于斜边的一半在直角三角形中的应用，以及直角三角形两锐角互余的性质．
CD=DG∴∠DGF=30°．
∵∠EKG+∠KGE=90°
∠KGE+∠DGF=90°
∴∠EKG=∠DGF=30°．∵2∠DKG+∠GKE=180°
∴∠DKG=75°．
分析：利用DF=
DG，可求出∠DGF，再求出∠GKE，利用2∠DKG+∠GKE=180°求出∠DKG的度数．点评：考查了30°角所对的直角边等于斜边的一半在直角三角形中的应用，以及直角三角形两锐角互余的性质．
练习册系列答案
阅读快车系列答案
相关题目
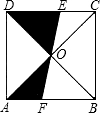如图，O是正方形ABCD的两条对角线BD，AC的交点，EF过点D，若图中阴影部分的面积为1，则正方形ABCD的周长为（ ）
如图，EF是正方形两对边中点的连线段，将∠A沿DK折叠，使它的顶点A落在EF上的G点，求∠DKG的度数．
