题目内容
在同一条直线上依次有A、B、C三地,甲、乙二人同时分别从A、B两地同向去C地,若甲、乙二人x小时候与B地的距离分别为y1千米、y2千米,且其图象如图所示,则甲、乙相遇时,甲走了 千米.
【答案】分析:先根据图象可以求出A地到B地的距离为3km,就可以求出甲的速度,就可以求出甲从B地到C地的时间就可以求出甲从B地到C地路程随时间的变化关系式,再根据图象求出乙从B地到C地的函数关系式就可以求出甲、乙相遇的时间,从而可以求出甲走的路程.
解答:解:由图象,得
甲的速度为:3÷0.5=6,
故甲从B地到C地用的时间为:9÷6=1.5.
设甲从B地到C地路程随时间的变化关系式y1=k1x+b1,乙从B地到C地路程随时间的变化关系式为y2=k2x,由图象得
 ,9=3k2,
,9=3k2,
解得: ,k2=3,
,k2=3,
则y1=6x-3,y2=3x,
当y1=y2时,则6x-3=3x,
解得:x=1.
故甲、乙相遇时,甲走的路程是:6×1=6km.
故答案为:6.
点评:本题考查了待定系数法求函数解析式的运用及一次函数交点坐标的求法的运用,行程问题速度= 的关系的运用,解答时求出一次函数的解析式是关键.
的关系的运用,解答时求出一次函数的解析式是关键.
解答:解:由图象,得
甲的速度为:3÷0.5=6,
故甲从B地到C地用的时间为:9÷6=1.5.
设甲从B地到C地路程随时间的变化关系式y1=k1x+b1,乙从B地到C地路程随时间的变化关系式为y2=k2x,由图象得
 ,9=3k2,
,9=3k2,解得:
 ,k2=3,
,k2=3,则y1=6x-3,y2=3x,
当y1=y2时,则6x-3=3x,
解得:x=1.
故甲、乙相遇时,甲走的路程是:6×1=6km.
故答案为:6.
点评:本题考查了待定系数法求函数解析式的运用及一次函数交点坐标的求法的运用,行程问题速度=
 的关系的运用,解答时求出一次函数的解析式是关键.
的关系的运用,解答时求出一次函数的解析式是关键. 
练习册系列答案
相关题目
 在同一条直线上依次有A、B、C三地,甲、乙二人同时分别从A、B两地同向去C地,若甲、乙二人x小时候与B地的距离分别为y1千米、y2千米,且其图象如图所示,则甲、乙相遇时,甲走了
在同一条直线上依次有A、B、C三地,甲、乙二人同时分别从A、B两地同向去C地,若甲、乙二人x小时候与B地的距离分别为y1千米、y2千米,且其图象如图所示,则甲、乙相遇时,甲走了 顶点,如菱形ABCD、EFGH、CIJK…,要求每个菱形的两条对角线长分别为4m和6m.
顶点,如菱形ABCD、EFGH、CIJK…,要求每个菱形的两条对角线长分别为4m和6m.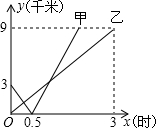 在同一条直线上依次有A、B、C三地,甲、乙二人同时分别从A、B两地同向去C地,若甲、乙二人x小时候与B地的距离分别为y1千米、y2千米,且其图象如图所示,则甲、乙相遇时,甲走了________千米.
在同一条直线上依次有A、B、C三地,甲、乙二人同时分别从A、B两地同向去C地,若甲、乙二人x小时候与B地的距离分别为y1千米、y2千米,且其图象如图所示,则甲、乙相遇时,甲走了________千米.