题目内容
如图,已知经过原点的直线AB与反比例函数y=kx-1（k≠0）图象分别相交于点A和点B,过点A作AC⊥x轴于点C,若△ABC的面积为4,则k的值为（ ）
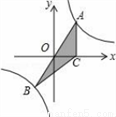
A. 2 B. 4 C. 6 D. 8
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
如图,已知经过原点的直线AB与反比例函数y=kx-1（k≠0）图象分别相交于点A和点B,过点A作AC⊥x轴于点C,若△ABC的面积为4,则k的值为（ ）
A. 2 B. 4 C. 6 D. 8
阅读快车系列答案
______ ,n=_______。
，将△ABC绕点C顺时针旋转，得到△A1B1C．
的正确结果是（ ）
C. 
D. 
