题目内容
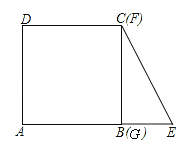
【题目】在圆O中，弦AB∥弦CD，AB=24，CD=10，弦AB的弦心距为5，则AB和CD之间的距离是_____ .
【答案】7或17
【解析】
根据题意画出图形，由于AB、CD在圆心的同侧或异侧不能确定，故应分两种情况进行讨论.
解：①当AB、CD在圆心的同侧，如图（一）所示时，过O作OE⊥CD，交AB于F，连接OA、OC，
由垂径定理可知AF=
AB=×24=12，CE=CD=×10=5，
在Rt△AOF中，OA=
=13；
所以OC=13，
在Rt△ACOE中，OE=
=12，
故EF=OE-OF=12-5=7；
②当AB、CD在圆心的异侧，如图（二）所示时，过O作OE⊥CD，交AB于F，连接OA、OC，
同（一）可知：OE=12，OF=5，EF=OE+OF=12+5=17；
故答案为：7或17．
练习册系列答案
相关题目
【题目】某校为了预测本校九年级男生毕业体育测试达标情况，随机抽取该年级部分男生进行一次测试（满分50分，成绩均记为整数分），并按测试成绩m（单位：分）分类：A类（45＜m≤50），B类（40＜m≤45），C类（35＜m≤40），D类（m≤35）绘制出如图所示的不完整条形统计图，请根据图中信息解答下列问题：
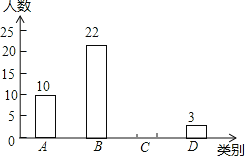
（1）a＝ ，b＝ ，c＝ ；
成绩等级 | 人数 | 所占百分比 |
A类（45 | 10 | 20% |
B类 | 22 | 44% |
C类 | a | b |
D类 | c |
（2）补全条形统计图；
（3）若该校九年级男生有600名，D类为测试成绩不达标，请估计该校九年级男生毕业体育测试成绩能达标的有多少名？
